Published by Minaxi1, Sanju Saini2, Garima Tiwari3, Deenbandhu Chhotu Ram University of Science and Technology, Murthal ORCID: 1. 0000-0003-4172-725X; 2. 0000-0003-1390-4861; 3. 0000-0002-3004-0375
Abstract. Blackout restoration is crucial to energy security and infrastructure resilience. Black-start procedures must be used to restore a power grid methodically. Grid recovery requires selecting the correct unit black-start optimization methods. Each Dijkstra shortest path approach determines a unit’s optimum recovery route after a large power loss. A full indication includes unit capacity, climbing rate, beginning power, recovery time, and route recovery capacitance. An exhaustive index. This index facilitates unit startup. We end with a unit black-start strategy using the optimal recovery route, unit start sequence, and unit start limitations. This method works in the IEEE30 node system simulation. Research suggests the black-start method may boost unit recovery and success. Black-start strategy performance is assessed for two prominent graph-based algorithms, Dijkstra and A. Unit black-start analysis is assessed for Dijkstra and A algorithms. Priorities include start sequence and recovery path optimization. Grid recovery efficiency and efficacy depend on performance measures. Optimization, route length, and calculation time improve process dependability and efficiency. Dijkstra’s simple, reliable approach works well in certain situations. The heuristic A* algorithm works well in certain cases. Both strategies are used in this paper to improve system performance. Explaining the power system’s peculiarities comparatively allows for selecting an algorithm.
Streszczenie. Przywracanie po awarii ma kluczowe znaczenie dla bezpieczeństwa energetycznego i odporności infrastruktury. Procedury czarnego startu muszą być stosowane w celu metodycznego przywracania sieci energetycznej. Przywracanie sieci wymaga wybrania prawidłowych metod optymalizacji czarnego startu jednostki. Każde podejście Dijkstry do najkrótszej ścieżki określa optymalną trasę odzyskiwania jednostki po dużej utracie mocy. Pełne wskazanie obejmuje pojemność jednostki, szybkość wznoszenia, moc początkową, czas odzyskiwania i pojemność odzyskiwania trasy. Wyczerpujący indeks. Ten indeks ułatwia uruchamianie jednostki. Kończymy strategią czarnego startu jednostki, wykorzystując optymalną trasę odzyskiwania, sekwencję uruchamiania jednostki i ograniczenia uruchamiania jednostki. Ta metoda działa w symulacji systemu węzłów IEEE30. Badania sugerują, że metoda czarnego startu może zwiększyć odzyskiwanie i sukces jednostki. Wydajność strategii czarnego startu jest oceniana dla dwóch wybitnych algorytmów opartych na grafach, Dijkstry i A. Analiza czarnego startu jednostki jest oceniana dla algorytmów Dijkstry i A. Priorytety obejmują sekwencję uruchamiania i optymalizację ścieżki odzyskiwania. Efektywność i skuteczność odzyskiwania sieci zależą od miar wydajności. Optymalizacja, długość trasy i czas obliczeń poprawiają niezawodność i wydajność procesu. Proste, niezawodne podejście Dijkstry sprawdza się w pewnych sytuacjach. Heurystyczny algorytm A* sprawdza się w pewnych przypadkach. Obie strategie są używane w tym artykule w celu poprawy wydajności systemu. Wyjaśnienie osobliwości systemu energetycznego w sposób porównawczy pozwala na wybór algorytmu. (Hybrydowe podejście do poprawy odtwarzania sieci)
Keywords: Hybrid Algorithms, Grid Restoration, Black-Start Recovery, Resilience Strategy.
Słowa kluczowe: Algorytmy hybrydowe, przywracanie sieci, odzyskiwanie po czarnym starcie, strategia odporności
1. Introduction
Recently, extreme weather disasters, malfunctioning power equipment, and human mistakes have caused largescale blackouts in domestic and worldwide power networks [1], [2]. Some examples include the 2019 Argentina “6.16” blackout, which impacted the whole nation [3], the 2021 Texas “2.15” power outage, and the 2022 Taiwan “33” island-wide blackout, which caused considerable economic losses. The guarded grid must be prioritized and restored to safeguard key municipal infrastructure from catastrophic disasters and external damages. The restoration control method is complicated and time-consuming. Developing a logical unit recovery route search technique may boost risk resilience and grid recovery time, which has major research and engineering consequences. Unit-optimal recovery route management alone cannot speed up power loss recovery.
Restoring power after a blackout uses black-start power. These generators are called “self-starting generators” because they can start themselves and restore power without external power [4]. The method of “unit start-up” in power generating involves black-starting producing units that cannot start themselves after a large power loss [5]. This method allows units to be reactivated and power-generating again, enabling load recovery and network reinstatement. A unit start-up approach includes both the recovery route and the unit start-up procedure; therefore, the two options are usually interrelated [6].
Power grid management and restoration need the blackstart technique to handle a difficult energy infrastructure situation: a complete blackout or loss of electricity throughout an electrical system. After such an event, power restoration is urgent and complicated. Restoring power generation and energy delivery to end-users, industrial sectors, and vital infrastructure is the biggest challenge [7]. Electrical systems need black-start strategies to provide continuous power delivery even under challenging conditions. This is because these groups reduce the immediate effects of a power loss and maintain social stability. Actively studying and optimizing these strategies helps solve dynamic power grid issues. Current power systems are reliable, and several methods have been developed to keep them safe [8], [9]. Large traditional synchronous generating units have been replaced by smaller distributed generation (DG) units in power systems. Distributed generating units powered by intermittent renewable resources affect several system activities, including dispatch and commitment. The power system’s high renewable energy content, along with unexpected weather occurrences and human error, increases the risk of blackouts. A series of linked failures might cause major power outages [10], [11].
Power restoration after a blackout requires black-start power. Production of electricity units may start generating electricity on their own to repair the network without external power. This helps when the entire system blacks out [4]. This application defines “unit start-up” as power-generating units that cannot start independently after an extensive loss. A black-start power supply does this. This assistance helps them produce electricity again, establishing the groundwork for network restoration and electrical load recovery [12]. The sequence of starting a unit and its recovery path must be carefully considered when creating a start-up strategy. These options are interrelated inside the approach [13]. The power system restoration decision-making process has traditionally included milestone stages. One research [14] explored a unit start-up technique to reduce restoration time at each phase. The second research [15] employed sequencing and traversal approaches to determine unit startup order. This restored more non-black-start units quickly. A later study [16] examined the device’s capacity recovery. According to [17], unit start-up includes recovery route charging time in the first phase. In [18], the elements that affect the unit’s black-start recovery are covered in detail. Calculating the unit’s recovery path using the shortest route technique and reference [17]. Distant operation coverage factor, line operation length, and recovery probability are studied [19]. After developing the function that forecasts line commissioning time, the unit start-up priority index determines the start-up order. Dijkstra’s method optimizes unit recovery route introduction. According to the literature [20], start sequence selection is multi-conceptualized. A data envelopment analytic technique using a backtracking algorithm solves the later unit selection issue. Goals include reducing unit recovery time and improving recovery success. Black-start procedures are crucial for power grid management to restore electricity after a complete blackout or system failure. They are crucial to electrical system reliability and continuity.
Domestic and international professionals optimize generator-starting procedures. Unit start-up and milestone parts of a power system restoration process of selection were created to shorten restoration times at all levels [21]. The literature [15] used traversal and sequencing algorithms to find the unit start-up sequence that restored the most non-black-start units fastest. The literature [22] was also concerned with optimizing system-generating capacity within a certain timeframe. Recovery route charging time is considered in the unit’s start-up function [23]. Unit restoration accuracy during black-start and recovery routes are examined using K shortest path analysis [18]. The literature addresses line operation time, remote operation coverage, and line recovery [24]. Create a unit start-up preference index and line commencement time expectation function to determine start-up order. While waiting, Dijkstra’s algorithm optimizes the unit as the starter’s recovery path. The literature [25] states that a multi-constrained backpack problem is resolved using data envelopment analysis and a backtracking method to identify the next unit to commence.
This study aims to shorten the unit’s recovery time and speed up its recovery. Prioritizing a black-start technique that considers the unit’s recovery trajectory and reactivation process will achieve the goal. Mathematical models for black-start power units are established in this article. These models have source and non-black-start power. It then finds the best way to start units after a major power loss using Dijkstra’s and A*’s shortest route algorithms. Also included are unit capacity, climbing rate, and beginning power. A complete black-start plan considers the unit start sequence, optimal recovery path, and unit start constraints. Simulation verifies this method’s efficacy. The black-start unit was enabled initially while constructing the power system restoration method. For grid restoration, this device supplies initial electricity. After each target generator activation, a recovery plan is determined. It lists the black-start units that will recharge each non-black-start unit. This research will provide a unique contribution to power grid resilience and black-start strategy design. Assuring grid recovery reliability and efficiency via algorithmic selection is the goal.
The building of mathematical models for non-black-start power sources and black-start power units, including gas turbines, starts this study. In the second portion, Dijkstra’s shortest path approach is used to find the best recovery route for units that must be started after a large power loss. It then mixes the recovery route with the unit’s capabilities, climb rate, beginning power, and other specifications. By considering unit initiation limits, a thorough black-start approach is created. This method depends on initial unit sequence and restoration efficiency. This approach is proven via simulation. Electricity is originally supplied by the black-start unit to restart the grid. Next, black-start units charge each non-black-start unit to gradually start the target generators. So-called Power System Restoration Planning.
2. Modeling used for present work
A 30-bus IEEE test setup with Every source in [26] collects system data. This data includes generator, load, shunt capacitor, and transmission line cost and emission coefficients. To accommodate non-smooth fuel cost functions, ramp rate coefficients have somewhat adjusted IEEE-30 bus system cost coefficients. At 100 MVA, the data is expressed.
2.1 Unit Recovery Path Search Using Dijkstra
A popular method for determining the shortest route in weighted networks is Dijkstra’s algorithm. Already at the origin, this technique finds the shortest path by spreading outward till the final vertex. This method relies on breadth-first search [27]. Once the grid is separated as a topology diagram G = (V, E), where V represents the graph’s vertices and E represents its branches, its loads, generators, lines, and transformers are removed as undifferentiated nodes. Weighing the branches according to Equation (1) takes into account the line’s charging time, transformer operation time, and capacitance value to construct the weighted topology graph.

From nodes i to j, wij represents the branch weight. Line charging and transformer recovery periods are included in the normalized branch recovery time, tij. Normalized capacitance value cij represents the branch’s recovery success rate between nodes i and j, and equation (2) shows how the adjacency matrix A outlines the grid topology diagram’s connection link.
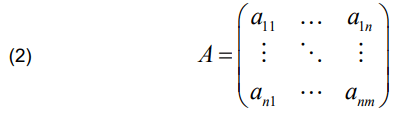
Node 1 is the black-start power node. Nodes 2–6 identify the unit to be started. Set VS = [1] contains the nodes that found the shortest route in the initial state. Vo = {2,3,4,5,6}, which includes all remaining nodes. Furthermore, D = [0,1,2,3, ∞, ∞] represents the appropriate distances between each node.
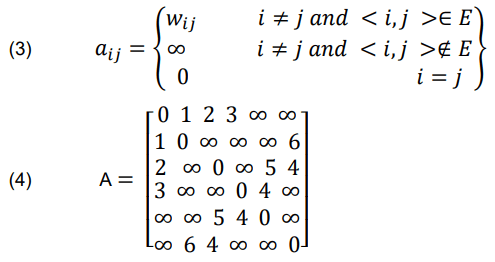
First, develop the adjacency matrix according to Equation (4). Node 2 is in set VS because set D shows it as the closest point to node 1. VS has [1,2], Vo has [3,4,5,6], and node 2’s shortest route is recorded.
Between the first and second nodes is 1 unit. According to the second row of the matrix of adjacency, node 2 is the intermediate node and seven distance separates nodes one to six. The initial specified D distance is greater than this figure. The distance set D now includes 0, 1, 2, 3, infinite, and 7. Set D finds node 3 closest to node 1, ignoring node 2. The quickest path to node 3 is documented by updating the VS and Vo lists to [1,2,3], [4,5,6]. The middleman is node 3. To alter D = [0,1,2,3,7,6], we add 7 and 6 from node 1 to nodes 5 and 6. Two units separate nodes 1–3. After refreshing VS = [1,2,3,4] and Vo = [5,6], node 4’s shortest route is collected. The revised D set places node 4 in Vo 3 distance from node 1. Nodes 1 and 5 are 7 distances apart because node 4 is the intermediate. The Vo node nearest to node 1 is node 6, 6 units away. We observe node 5’s shortest path and alter VS = [1,2,3,4,6] and Vo = [5]. As node 1 and node 6 are not directly connected, the quickest path from node 5 is quickly revealed. D comprises the shortest distances: [0, 1, 2, 3, 7, 6]. The process flow of pathfinding. Additionally, S is the shortest route matrix.
2.1.1. Integrated Index of Unit Start-Up Sequence
a) Index of Unit Characteristics
When selecting units to recover in order, use these criteria [28]:
1) Hot-start units are restored first to optimize hot-starting.
(2) When there is insufficient power to create electricity during system recovery, units with low starting powers are prioritized for a smooth start.
(3) For fast system recovery, units with faster-increasing rates are restored first.
(4) High-recovery units are prioritized to ensure power production capacity.
A unit characteristic index is calculated using unit capacity, climbing rate, and initial power in Equation (5).
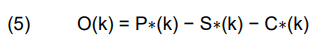
The characteristic index of the kth unit is “O(k)”. “C(k)” is the normalized climb rate, “S(k)” is capacity, and “P(k)” is its beginning power. Normalization is shown in Equation (6).
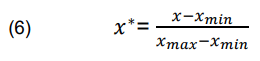
Where, xmin, xmax, x* stand for the minimum, maximum, and normalized values of x, y, and x* respectively. This model has the following variables defined: the amount of time the device takes to start up, in seconds; tc; the moment it launches its power delivery and links to the grid; tmax, the duration of time it delivers its highest level of active power externally; K, the pace at which the unit is rising; Pst, the unit’s active power while using the plant as its power source; KN, the unit’s average climbing rate; Furthermore Pmax, the unit’s maximum active power.
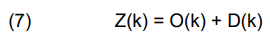
The kth unit’s composite index is denoted by Z(k), its characteristic index is denoted by O(k), and its distance index is represented by D(k).
b) Restrictions on Unit Startup
The time constraint of a start-up:
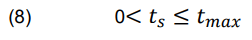
The variable “tmax” represents the upper limit for the hot-start time of the unit, whereas “ts” provides the starting time of the non-black-start unit. It represents the maximum time the unit may be hot-started before failing. The unit must meet Equation (9) (minimum cold-start time) if its hot-start time exceeds it.
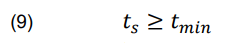
The variable “ts ” denotes the initial time of the non-black-start unit, while “tmin“ reflects the minimum time required for the non-black-start unit to reach its operating temperature.
c) Start-up power constraint
The following equation can be written as p is the system’s black-start unit count, The system’s restored non-black-start unit count is denoted by q,
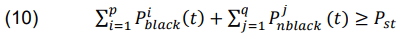
the active power output from the ith black-start unit at time t is represented by Pi(t), the active power output from the jth non-black-start unit at time t is represented by Pj(t), and the start power needed to start the next unit is called Pst.
d) Constraints on the start/stop condition of the unit It is expected that once the unit has been started, it will continue to function without any further shutdowns. Therefore,
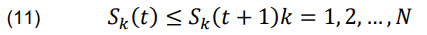
The variable Sk(t) represents the status of unit k at time t, where a value of 1 indicates that the unit has started and a value of 0 indicates the opposite.
e) Power constraints
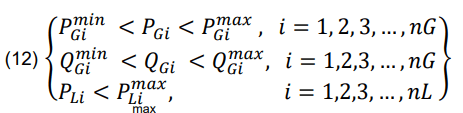
where PGi denotes the generator set’s maximum active power output and Pmin denotes the lowest permitted active power output.
Gi denotes the generator set’s active power; PGi denotes the maximum permissible output of active power; QGi denotes the generator set’s reactive power; Qmin denotes the lowest permissible output of reactive power; Qmax denotes the maximum permissible output of reactive power; Li denotes the active power transmitted by the ith line; and Pmax denotes the maximum permissible power available.
f) Voltage constraints
The values of Umin, Umax, and Ui represent the lower and upper voltage limits, respectively, of the ith node, Ui being its magnitude of the voltage value.
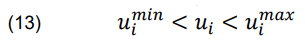
2.1.2. Unit Start-Up Process The unit starts policy development.
Here’s how to start the unit. Analyze the grid’s topology and attributes. Transformers, lines, generators, and loads are branches and nodes. Weight branches by line capacitance, transformer working time, and line charging time. Weighted topology diagrams with adjacency matrix A outcome from this idea.
Dijkstra’s method is used to each non-black-start unit’s distance index to discover the unit’s recovery route’s shortest path. Look at the sequence of the units’ starts to determine which should be launched next, disregarding those with a black start. Examine power, voltage, hot-start time, and start power limits. Unqualified units are either placed at the start of the beginning sequence or through the cold start process until they fulfill the standards. Update the system’s recovery status while getting the fastest-starting units. A* (A star) is a popular algorithm used for pathfinding and optimization in various domains, including analyzing recovery paths and start sequences [29], [30]. A* is an informed search algorithm that combines the benefits of Dijkstra’s algorithm and heuristics to efficiently find the shortest path while exploring the graph [31], [32]. Here’s how A* can be applied to analyze recovery paths and start sequences:
2.1.3. Recovery Paths in a Network
In network management and fault recovery, A* can be used to find the most efficient recovery paths for restoring network connections after a failure. This involves finding a path that minimizes a specific cost while considering the network topology.
• Source Node: The point of network failure.
• Destination Node: The destination for rerouted traffic.
In both scenarios, A* is employed to efficiently find optimal paths or sequences by using heuristics to guide the search process. The choice of an appropriate heuristic can significantly impact the algorithm’s performance and accuracy in finding the optimal solution.
The aforementioned advantages make A* a powerful instrument for addressing a diverse array of issues that include the identification of the optimal route or solution inside a network or graph. The versatility, effectiveness, and assurance of optimality that it offers make it a preferred option for several applications.
2.2. Difference between Dijkstra’s and A* Algorithms
Dijkstra’s algorithm and A* (A-star) algorithm are two popular graph search algorithms used for finding the shortest path between two nodes in a graph. Here’s a tabular comparison of the main differences between these two algorithms:
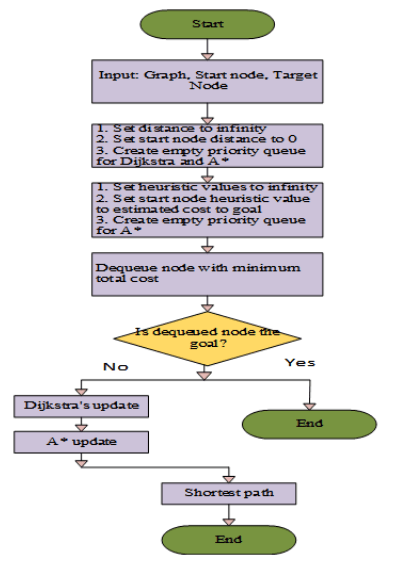
Fig. 1 Hybrid Dijkstra and A* Algorithm 2.2.1. Unit Recovery Path Search Using Hybrid Dijkstra and A* The combination of Dijkstra’s algorithm and A* (A-star) algorithm for unit recovery path search is often referred to as the Hybrid Dijkstra-A* algorithm. Both Dijkstra’s and A* algorithms are popular pathfinding algorithms used in computer science and robotics for finding the shortest path between two points in a graph or grid. The hybrid nature of this algorithm comes into play by combining the results of Dijkstra’s and A. Instead of using A throughout the entire search, you can leverage the information obtained from Dijkstra to guide the search. During the A* search, if the algorithm encounters a node that has already been visited by Dijkstra’s and if the current path to that node is shorter than the path found by Dijkstra’s, you can update the information for that node using the shorter path. Fig 1 shows the Hybrid approach of restoring path. This way, the algorithm benefits from the efficiency of A* while incorporating the additional information provided by Dijkstra to improve the accuracy of the pathfinding.
3. Result Discussion
The result discussion serves as a A* (A-star) and Dijkstra’s algorithm are used in the hybrid method to route recovery in a system graph to maximize the shortest path search. Dijkstra’s method ensures that the shortest route is found by investigating every option, and A* employs heuristics to effectively direct the search. With g(n) standing for the cost from the start node, h(n) for the heuristic estimate to the objective, and f(n)=g(n)+h(n) for the total cost, the hybrid method preserves node information. The method updates costs and investigates neighbors while iteratively choosing nodes from a priority queue with the lowest f(n). This hybrid method effectively solves the route recovery problem in a system graph by balancing the effectiveness of A* with the dependability of Dijkstra’s.
3.1. Capacities and ON time of Each Node
Incorporating capacity values into the hybrid algorithm ensures that the path recovery process aligns with real-world resource constraints. The combination of Dijkstra’s and A* with capacity awareness leads to more efficient and practical solutions in complex network scenarios. Incorporating on-time values into the hybrid algorithm ensures that the path recovery process aligns with temporal dynamics. The combination of Dijkstra’s and A* with on-time awareness leads to more informed and adaptive pathfinding solutions in dynamic environments.
3.2. Comparison Graph
The comparison graph shows the different structures graphs and nodes explored in all three algorithms shown in figure 2 and table 1.
Table 1. Comparison of Algo with Nodes and Distances

Table 2. Comparison of Algo with Time

The first section compares the length of paths found by the hybrid algorithm, A, and potentially Dijkstra’s if included in the comparison. The second section compares the number of nodes explored during the pathfinding process by the hybrid algorithm, A, and Dijkstra’s. The table 2 and the time and nodes performances for each algorithm across different scenarios.
In each scenario, the hybrid algorithm provides better results, striking a balance between optimality (Dijkstra) and efficiency (A).
4. Conclusion and Future Scope
In conclusion, Dijkstra and A algorithms in black-start techniques and recovery route optimization provide grid resilience in a complex but realistic way. We improve power grid restoration efficiency, adaptability, and reliability by combining both methods, reducing downtime and strengthening the electrical infrastructure. The inclusion of cutting-edge algorithms will help our grids withstand unexpected obstacles as power system management advances and some future directions are:
1. Real-Time Data Integration
2. Quantum Computing Applications
3. Integrate cybersecurity measures into resilience plans
4. Optimize algorithms
5. Enhance Smart Grid Synergies
6. Incorporate adaptive control mechanisms into algorithms to modify performance and adaptability.
7. Community-Based Resilience Methods
8. Quantifiable Resilience measures
9. Inter-sector Integration
Future grid resilience directions strive to provide flexibility, efficiency, and security in the face of changing problems and technology.
REFERENCES
[1] J. Zhao, H. Wang, Y. Liu, Q. Wu, Z. Wang, and Y. Liu, Coordinated Restoration of Transmission and Distribution System Using Decentralized Scheme, IEEE Transactions Power System, 34 (2019), No. 5, 3428–3442.
[2] M. S. Javed, T. Ma, J. Jurasz, and M. Y. Amin, Solar and wind power generation systems with pumped hydro storage: Review and future perspectives, Renewable Energy, 148 (2020), 176–192.
[3] P. Yuan et al., Analysis and Enlightenment of the Blackouts in Argentina and New York, in Chinese Automation Congress (CAC), Hangzhou, China: IEEE, (2019), 5879–5884.
[4] Y. Liu, R. Fan, and V. Terzija, Power system restoration: a literature review from 2006 to 2016, Journal of Modern Power Systems and Clean Energy, 4 (2016), No. 3, 332–341.
[5] A. Ketabi, A. Karimizadeh, and M. Shahidehpour, Optimal generation unit’s start-up sequence during the restoration of power system considering network reliability using bi-level optimization, International Journal of Electrical Power & Energy Systems, 104 (2019), 772–783.
[6] C. Shen, P. Kaufmann, and M. Braun, Optimizing the generator start-up sequence after a power system blackout, in 2014 IEEE PES General Meeting, Conference & Exposition, National Harbor, MD, USA: IEEE, (2014), 1–5.
[7] Y. Zhao et al., Energy storage for black start services: A review, International Journal of Minerals, Metallurgy and Materials, 29 (2022), No. 4, 691–704.
[8] H. Bevrani, M. R. Feizi, and S. Ataee, Robust Frequency Control in an Islanded Microgrid: H∞ and μ-Synthesis Approaches, IEEE Transaction Smart Grid, (2015).
[9] A. Fathi, Q. Shafiee, and H. Bevrani, Robust Frequency Control of Microgrids Using an Extended Virtual Synchronous Generator, IEEE Transaction Power System, 33 (2018), No. 6, 6289–6297.
[10] A. Halik, Y. Syam, A VECM Analysis of the Impact of Economic Growth and Investment on Electricity Consumption in Indonesia, Przegląd Elektrotechniczny, 2(2024), 140-144.
[11] P. Yuan et al., Analysis and Enlightenment of the Blackouts in Argentina and New York, in 2019 Chinese Automation Congress (CAC), Hangzhou, China: IEEE, (2019), 5879–5884.
[12] J. Su, C. Chen, and Z. Bie, Optimal Generator Start-Up Sequence Strategy Considering Renewable Energy Participation, in The Proceedings of the 17th Annual Conference of China Electrotechnical Society, 1014 (2023), 934–945.
[13] S. Zhai, H. Wang, Y. Shan, and X. Zhang, Optimal Generator Start-up Sequence with Active Distribution Networks Considering Recovery Path, in 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China: IEEE, (2021), 472–478.
[14] S. Alhamid, O. hamandouch, A. Darwish, A hybrid Bees Algorithm to Enhance the Performance of Radial Distribution Systems, Przegląd Elektrotechniczny, 2(2024), 193-196.
[15] K. Liang, H. Wang, D. Pozo, and V. Terzija, “Power system restoration with large renewable Penetration: State-of-the-Art and future trends,” International Journal of Electrical Power and Energy Systems, 155 (2024), 109494.
[16] En Lu, Ning Wang, Zhijun Qin, Haoming Liu, and Yunhe Hou, Black-start strategy for power grids including fast cut thermal power units, in 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC: IEEE, (2013), 1–5.
[17] V. Singhvi, D. Ramasubramanian, S. Uppalapati, W. Baker, and E. Farantatos, An Analytical Procedure to Evaluate Optimal Restoration Path with Multiple Blackstart Units Including Inverter Based Resources, in 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA: IEEE, (2021), 1–5.
[18] J. Zhao et al., Research on the Unit Black-Start Strategy Considering Recovery Path and Start Sequence, Sustainability, 14 (2022), No. 20, 13057.
[19] T. Wang, H. Zhu, Z. Wang, Y. Wang, N. Sun, and Y. Dong, Multi-objective Optimization of Unit Restoration During Network Reconstruction Based on DE-EDA, in 2020 IEEE 3rd International Conference on Electronics and Communication Engineering (ICECE), Xi’An, China: IEEE, (2020), 102–106.
[20] A. Ketabi, A. Karimizadeh, and M. Shahidehpour, Optimal generation unit’s start-up sequence during restoration of power system considering network reliability using bi-level optimization, International Journal of Electrical Power & Energy Systems, 104 (2019), 772–783.
[21] Y. Hou, C.-C. Liu, K. Sun, P. Zhang, S. Liu, and D. Mizumura, Computation of Milestones for Decision Support During System Restoration, IEEE Transactions on Power Systems, 26 (2011), No. 3, 1399–1409.
[22] En Lu, Ning Wang, Zhijun Qin, Haoming Liu, and Yunhe Hou, Black-start strategy for power grids including fast cut thermal power units, in 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC: IEEE, (2013), 1–5.
[23] X. Gu, G. Zhou, S. Li, and T. Liu, “Global optimization model and algorithm for unit restarting sequence considering blackstart zone partitioning,” IET Generation, Transmission & Distribution, 13 (2019), No. 13, 2652–2663.
[24] A. Ketabi, H. Asmar, A. M. Ranjbar, and R. Feuillet, An approach for optimal unit’s start-up during bulk power system restoration, in LESCOPE 01. 2001 Large Engineering Systems Conference on Power Engineering. Conference Proceedings. Theme: Powering Beyond 2001 (Cat. No.01ex490), Halifax, NS, Canada: IEEE, (2001), 190–194.
[25] D. Hazarika and A. K. Sinha, “Power system restoration: planning and simulation,” International Journal of Electrical Power & Energy Systems, 25 (2003), No. 3, 209–218.
[26] G. Bagha and A. Kumar, Load Flow Analysis of IEEE-30 Bus System Using FACTS Device, SSRN Electron. Journal, (2020).
[27] Zhou Yunhai and Min Yong, Optimal algorithm for system reconstruction, in Proceedings. International Conference on Power System Technology, Kunming, China: IEEE, (2002), 201–203.
[28] L. Xu, Q. Guo, Y. Sheng, S. M. Muyeen, and H. Sun, On the resilience of modern power systems: A comprehensive review from the cyber-physical perspective, Renewable and Sustainable Energy Review, 152 (2021), 111642.
[29] C. Ju, Q. Luo, and X. Yan, Path Planning Using an Improved A-star Algorithm, in 2020 11th International Conference on Prognostics and System Health Management (PHM-2020 Jinan), Jinan, China: IEEE, (2020), 23–26.
[30] D. Foead, A. Ghifari, M. B. Kusuma, N. Hanafiah, and E. Gunawan, A Systematic Literature Review of A* Pathfinding, Procedia Computer Science, 179 (2021), 507–514.
[31] D. Rachmawati and L. Gustin, Analysis of Dijkstra’s Algorithm and A* Algorithm in Shortest Path Problem, Journal of Physics: Conference Series, 1566 (2020), No. 1, 012061.
[32] S. Erke, D. Bin, N. Yiming, Z. Qi, X. Liang, and Z. Dawei, An improved A-Star based path planning algorithm for autonomous land vehicles, International Journal of Advanced Robotic Systems, 17 (2020), No. 5, 172988142096226.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 100 NR 9/2024. doi:10.15199/48.2024.09.13