Published by 1. Afaneen Anwer Abbood1, 2. Hanan Mikhael D. Habbi2, University of Technology-Iraq, Baghdad, (1) , University of Baghdad, Dept. Of Electrical Engineering, Baghdad, Iraq (2)
ORCID: 1. 0000-0003-3995-8307; 2. 0000-0003-4982-4345
Abstract. Renewable energy can make the utility grid unstable by causing some problems, such as frequency fluctuations, voltage surges, and power instability because of the inconsistency of renewable energy resources. This paper focused on studying the effect of intermittent renewable energy represented by a PV-integrated grid on the frequency system response and grid voltage surge. Heuristic Optimization methods, Teaching learning-based optimization (TLBO), and particle swarm optimization (PSO) have been utilized to optimize the penetration of PV energy enhancing the supply frequency response. Both optimization methods have been implemented with different values of irradiance. Although they have similar performances, the simulation result showed that the TLBO method has a slightly better low-frequency oscillation than the PSO method. It is found that the TLBO algorithm presents a good power quality response of the grid-connected system. This is due to the fact of TLBO is faster than the PSO algorithm because it does not need specific parameters. The system is applied to a feeder in a distribution network in Baghdad power sector. The results are obtained by using the MATLAB package.
Streszczenie. Energia odnawialna może spowodować niestabilność sieci elektroenergetycznej, powodując pewne problemy, takie jak wahania częstotliwości, skoki napięcia i niestabilność mocy z powodu niespójności zasobów energii odnawialnej. W artykule skupiono się na badaniu wpływu przerywanej energii odnawialnej reprezentowanej przez zintegrowaną sieć fotowoltaiczną na odpowiedź systemu częstotliwości i udary napięcia sieciowego. Aby zoptymalizować przenikanie energii fotowoltaicznej, zwiększając charakterystykę częstotliwościową zasilania, zastosowano metody optymalizacji heurystycznej, optymalizacji opartej na uczeniu się (TLBO) i optymalizacji roju cząstek (PSO). Obie metody optymalizacji zostały zaimplementowane przy różnych wartościach natężenia napromieniowania. Chociaż mają one podobne właściwości, wynik symulacji pokazał, że metoda TLBO charakteryzuje się nieco lepszymi oscylacjami w zakresie niskich częstotliwości niż metoda PSO. Stwierdzono, że algorytm TLBO zapewnia dobrą odpowiedź dotyczącą jakości energii w systemie podłączonym do sieci. Wynika to z faktu, że TLBO jest szybszy od algorytmu PSO, ponieważ nie wymaga określonych parametrów. System stosowany jest w polu zasilającym w sieci dystrybucyjnej w sektorze energetycznym Bagdadu. Wyniki uzyskuje się za pomocą pakietu MATLAB. (Optymalizacja heurystyczna penetracji energii fotowoltaicznej w celu zapewnienia odporności na wahania częstotliwości systemu)
Index Terms: Power system distribution, Frequency fluctuations, Teaching Learning Based Optimization (TLBO), PSO
Słowa kluczowe: Dystrybucja systemu elektroenergetycznego, wahania częstotliwości, optymalizacja oparta na nauczaniu (TLBO), PSO
Introduction
Despite the ease of use of renewable energy due to the impulses of nature regularly renewable energy has many prospective advantages over fossil power generation [1-3], the rapid or intermittent penetrations of renewable energy resources such as wind energy and solar PV energy cause serious problems to the power system fluctuations in the voltage and system frequency [4-6]]. These problems require accurate and satisfactory solutions to ensure that the integrated grid works efficiently. On the other hand, the penetration of wind energy (renewable energy resource) may lead to a percentage change in the frequency performance of the power system [7, 8]. Many researchers discussed these problems. Ref [9] proposed a tuned virtual filter that connected to a wind energy integrated grid to mitigate the system frequency fluctuations. It has been shown that the proposed system does not affect the efficiency of wind energy. Ref [10] studied and compared the number of strategies to control the drop frequency and the step response for a high PV system penetration without curtailing solar PV energy, it explored the storage energy for initial frequency response and implemented the strategies on the Texas grid, USA. Rajiv K and M Akbari,[11] suggested a PV-STATCOM to enhance the frequency and power system stability deviation by combining two controllers’ rapid frequency control and power oscillation damping to control the real power. Whereas Ref [12] designed and implemented the combination of the two controllers for simply real power control of Type 4 wind turbines. Mao Yang, et.al. [13] proposed a tabular model to study and analyze the effects of constraints of the renewable energy grid model in terms of output power, voltage, and frequency fluctuations.
On the other hand, some researchers minimized the frequency deviation using different intelligent techniques such as [14-19] a fuzzy-based frequency control incorporating the active frequency response constraints into the optimal development model, while [20] proposed the Mixed Integer Linear Programming (MILP) method. Refs. [21-23] developed a real-time nonlinear curve fitting maximum power point tracking. This paper proposed an integrated grid system for a distribution feeder to migrate to a distributed generation model for higher availability of electricity from a variety of sources (solar, and DG power). The effect of the intermittent load on the system frequency percentage changes for the PV-integrated grid was studied. The algorithms were applied to a feeder in the Baghdad power sector in a distribution network. The system includes 15kW, fixed PV solar panels, combined with a DC- AC inverter of 25kW, and the 15-kW annual hourly peak demand, with peak day energy use of 3.85kWh. The total PV generation is 96.68kW (4.03kW average).
Simulation Model
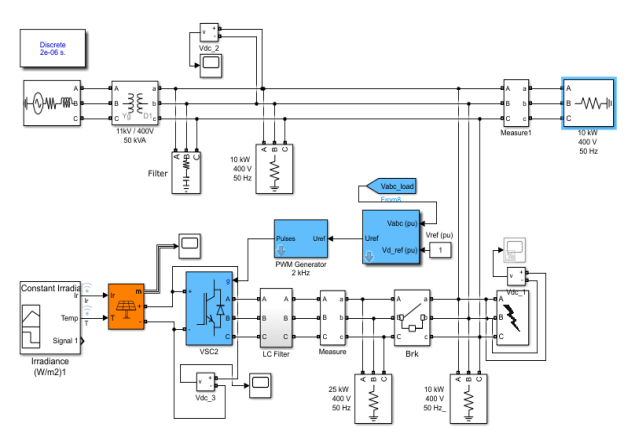
The proposed method depends on the amount of total power generated from each energy resource that is connected to the feeder. The optimal generated power from each source annually might cover the required demand load, considering the weather variations. The whole proposed system is shown in Fig.1. The frequency and grid voltage responses under different values of irradiance were compared based on two optimization methods (TLBO and PSO).
Also, the statistical distribution over time was analysed according to the availability of resource data (DG size and solar PV energy penetration at a specific period). The simulation layers include energy resources, data information, and optimization algorithms as shown in Fig.2.

The PV system efficiency is given in Equation (1)
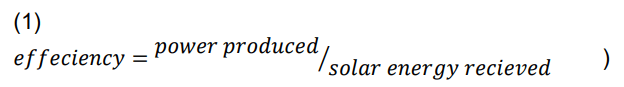
The annual capacity factor is given in Equation (2)

The annual capacity factor can be (0.25- 0.3) depending on the weather.
Heuristics Optimization
Heuristics optimization uses combinational computations, which depend on the practical experience of the system that will be studied. There are some specific cases that will be discussed in detail in the results section. The goal is to make the difference between the capacity produced from the energy sources attached to the system close to the requirements of the load and the utilization of capacity produced from solar cells in peak load processing. In the case of cloudy weather conditions or in the event of sunset (night-time), as the solar cells do not produce energy, therefore, the system will depend on the national grid.
Teaching Learning-Based Optimization (TLBO)
The influence of the teacher has affected the output of the learners. This algorithm does not require the specific parameters as in PSO algorithm. Therefore, it could obtain the optimum values with less computation time and operations [1], [2]. There are two modes for TLBO: the teacher phase and the learner phase. Let gets start to explain these modes:
1) Teacher Phase
To understand the modelling of this algorithm, it might illustrate the following factors: min F(x) limits
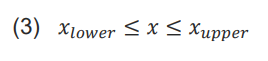
N=No. of iterations; P=size of population; Fval=determined by TLBO ; BFval=the best fitness function value in each iteration; Po= the population at the end of the specified no.of iteration.; For gen=1 to N;
Partner selection for all students begin of the teacher factor generation of a new solution bounding of the solution evaluation of the solution Greedy selection
2) Leader phase
Generation of a new solution Bounding of the solution evaluation of the objective function greedy selection
Power balance of the microgrid
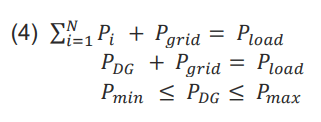
In this paper, it takes 5 learners and 2 subjects. That means the decision variables are 2. According to our decision variables, the objective function or test function becomes:

After that, it can calculate the values of Pgrid and PDG taking the values of N=50, and P=10. According to the size of the iteration N=50, and it will start the evaluation before the start of the iteration. Since, the TLBO has two parameters which are the size of the population (P) and the size of the iteration (N). Therefore, the convergency of the TLBO does not change or vary. That’s results to minimize the oscillation in the power mismatch equality between the generation and the demand will be slightly slow.
Particle Swarm Optimization (PSO)
An evolutionary computation algorithm PSO gives the optimal solution of the energy penetration from a variety of energy resources [3]. It needs an initialization of the system parameters, no of the particles = 100 and the maximum iteration time is 0.2sec as well as the parameters of the power demand and weather conditions. Then, each particle will generate the initial speed I from 1 to 100 to obtain the global and best values. After that, each particle is updated with its speed to get the optimal value. Obtaining the optimal value of the grid and demand power for the energy management of a microgrid using PSO takes a time to reach the optimal value, that will show an oscillation in the quality of the result. In other word, PSO has a low convergence for the frequency response in energy management microgrid system. In contrast, the implementation of the PSO will be simple than the TLBO method [4]. Nevertheless, PSO has an ability to get a local convergence that will results to be a slow computation and will effect on the response quality.
Results And Discussion
The complete system shown in Fig 1 is implemented with MATLAB/Simulink with a constant irradiance (1000W/m2). Fig. 3 shows the frequency response and the frequency deviation for the PSO algorithm. It can be illustrated from the results that; the frequency response has an oscillation down to 48Hz and it takes about 10sec to reach a steady state value at 50Hz. This oscillation is because of the penetration of the power from the solar PV into the microgrid. Fig. 4 shows the grid voltage in volt and per unit. The irradiance and temperature values are kept constant taking as 1000W/m2 and 25Co respectively. The parameters for Baghdad feeder are shown in Table 1. It is cleared from Fig. 4 that the grid voltage (Vg) will be stable within a short time based on TLBO. Meanwhile, the PSO takes a time to solve the oscillation problem.
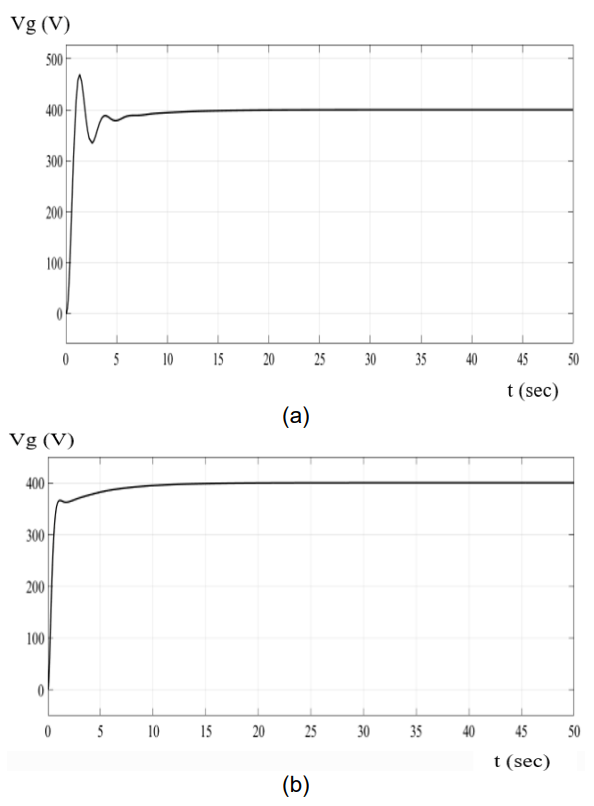
It can be observed from Fig.4 (a) and (b) when the irradiance is kept constant that the frequency deviations for TLBO and PSO frequency response can be detected and eliminated within 5 sec. The simulation results for the grid voltage results using PSO as shown in Fig. 5(a) take about 5sec to reach its rated value while the grid voltage as shown in Fig.5 (b) using TLBO algorithms have a fast response and reaches the grid voltage (400V) abruptly without an oscillation.

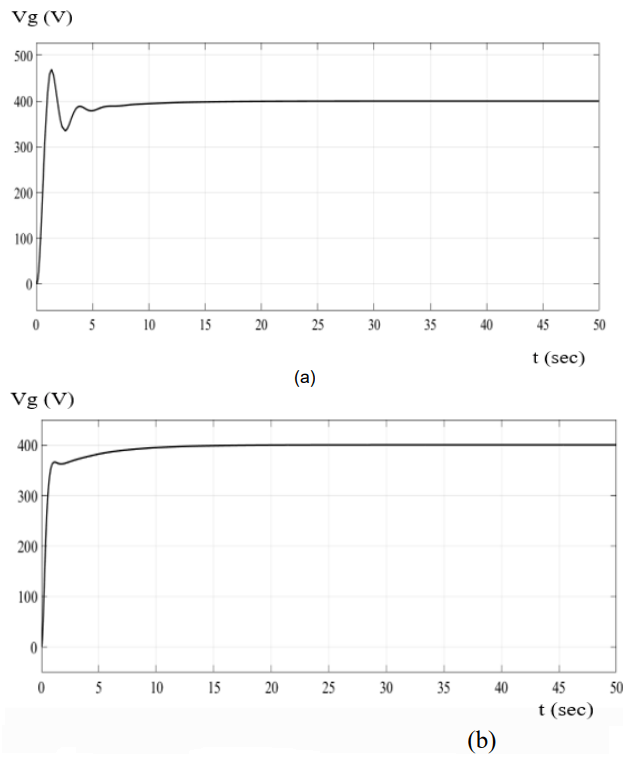
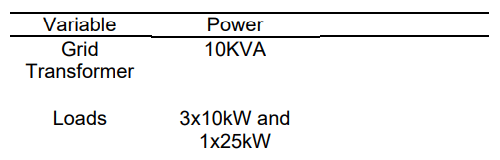
Table 1. The Parameters of the Baghdad feeder
Variable Irradiance
In this section, the effect of changing the irradiance on the frequency response and the voltage grid have been studied using two optimization algorithms (PSO and TLBO). The irradiance applied to PV solar (1000W/m2 at zero sec to 500W/m2 at 1.5 sec) as shown in Fig.5.
When the PV solar irradiance is suddenly changed from 1000W/m2 to 500 W/m2 at 1.5sec as shown in Fig. 6, the frequency response for PSO and TLBO methods as shown in Fig. 6. The frequency response from TLBO has a good and an optimal control. However, it is obvious that the change in frequency response is rapidly slow down with TLBO algorithm. While the frequency response of the microgrid system from the PSO results takes a long time to settle down to 50Hz. In addition, the amplitude of the frequency oscillations is high for the PSO results compared with that of TLBO algorithms. That is the frequency response for TLBO frequency response can be detected and eliminated within less than 0.25 sec, while that of the PSO results will be more than 5 sec to settle down. Not only the system response of the TLBO algorithm is faster than that of the PSO results but also the overshooting in the frequency response has better results using TLBO. The results show satisfactory observations of the fluctuations elimination and oscillation amplitude within a considerable time.
The simulation results when the irradiance is changed as shown in Fig. 7, the grid voltage results using PSO as shown in Fig.7 (a) take about 5sec to reach its rated value while the grid voltage as shown in Fig.7 (b) using TLBO algorithm have a fast response and reaches the grid voltage (400V) abruptly without an oscillation.
The comparison of frequency response using PSO and TLBO optimization methods under sudden changes in PV solar irradiance reveals that TLBO demonstrates superior performance with faster and more stable responses, effectively eliminating fluctuations and minimizing overshooting. In contrast, PSO exhibits slower settling time and higher amplitude of oscillations, making it less efficient in achieving grid stability. TLBO’s ability to quickly regulate frequency and its reduced computational burden make it a promising and practical choice for real-world applications in microgrid systems, with the potential for further refinement to enhance its performance.


It can be concluded that the sudden decrease in irradiance results in the rapid decrease of active power output from PV solar systems. Consequently, the power deviation (difference between load power and generated power) returns to zero. However, under the PSO method, it is obvious that the amplitude of frequency response oscillation and grid voltage surges is higher using PSO algorithm compared to that of TLBO algorithm. Since it can reach the optimal value with a significant value of time computation with less oscillation or disturbances on the obtained responses.
Conclusion
This paper considers two optimization methods PSO and TLBO to optimize the penetration of the power to the microgrid system through the PV energy resources. This penetration of power influences the grid frequency and grid voltage surges. However, it is a challenge to perform MPPT with a variable irradiance. The paper compares the frequency and voltage oscillation of the microgrid using two optimization methods (PSO and TLBO) under different irradiance values. PSO algorithm has a low convergence for the frequency response in energy management microgrid system. The implementation of the PSO is simple than the TLBO method. Nevertheless, PSO has an ability to get a local convergence that led to a slow computation and that will influence the response quality. On the other hand, the TLBO has two parameters which are the size of the population (P) and the size of the iteration (N), the size of the iteration is proposed to be N=50, and it is starting the evaluation before the starting of the iteration. Therefore, the convergence of the TLBO does not change or vary. That’s results to minimize the oscillation in the power mismatch equality between the generation and the demand. It can be concluded that the TLBO algorithm gives an optimal value of the power that can be obtained from the solar PV energy resource. It can significantly observe the reduction of the frequency oscillation and can further improves the power quality with MPPT based on TLBO with a significant value of time computation with less oscillation or disturbances on the frequency and voltage responses. It is found that the TLBO algorithm presents a good quality convergence to the frequency and better voltage response of the grid connected system.
REFERENCES
[1] H. L. W. a. W. G.Scott, “Distributed Power Generation, planning and evaluation”, (2000), Publisher: New York : Marcel Dekker.,” 2000.
[2] R. Takahashi, Umemura, A., Tamura, J., Kimura, M., & Hino, N, “Simulation analyses of stabilization control of power system frequency fluctuations resulting from wind farm output by gas turbine thermal power plant. https://doi.org/10.1002/eej.23321,” Electrical Engineering in Japan, vol. 214, no. 2, 2021.
[3] J. Hossain, & Mahmud, A, ” Renewable Energy Integration. https://doi.org/10.1007/978-981-4585-27-9,” Springer Singapore., 2014.
[4] B. Al Kindhi, Lasminto, U., Triana, M. I., Damarnegara, S., & Anavatti, S. G. , “4. Sensor and internet of things based integrated inundation mitigation for smart city. International Journal of Electrical and Computer Engineering (IJECE), 13(3), 2695. https://doi.org/10.11591/ijece.v13i3.pp2695-2703,” 2023.
[5] Ahmed Abbas Abdul-Hamza and Hanan M. Habbi, “[6] (2016). Fault detection and diagnosis based on artificial neural network. International Journal of Scientific & Engineering Research, VOL. 7, NO. 5, 2016, PP- 1690-1697. https://www.ijser.org/research-paper-publishing-may2016_page8.aspx.,” 2016.
[6] T. S. Tagare, & Narendra, R, “Lifetime enhanced energy efficient wireless sensor networks using renewable energy. https://doi.org/10.11591/ijece.v13i3.pp3088-3098,” International Journal of Electrical and Computer Engineering (IJECE),, vol.13, no. 3, p. 3088, 2023.
[7] M. G. Dozein, Chaspierre, G., Mancarella, P., Panciatici, P., & van Cutsem, T. , ” Frequency Response From Solar PV: A Dynamic Equivalence Closed-Loop System Identification Approach,https://doi.org/10.1109/JSYST.2021.3051938,” IEEE Systems Journal,, vol. 16, no. 1, pp. 713–722, 2022, doi: https://doi.org/10.1109/JSYST.2021.3051938.
[8] L. Zhou, Chen, Y., Luo, A., Guerrero, J. M., Zhou, X., Chen, Z., & Wu, W., “Robust two degrees-of-freedom single-current control strategy for LCL-type grid-connected DG system under grid-frequency fluctuation and grid-impedance variation. https://doi.org/10.1049/iet-pel.2016.0120,” IET Power Electronics,, vol. 9, no. 14, pp. 2682–2691, 2016.
[9] I. Isknan, Asbayou, A., Hamid Adaliou, A., Ihlal, A., & Bouhouch, L., “Comparative study and simulation of advanced MPPT control algorithms for a photovoltaic system. https://doi.org/10.11591/ijeecs.v30.i1.pp46-56.,” Indonesian Journal of Electrical Engineering and Computer Science,, vol. 30, no. 1, p. 46, 2023.
[10] A. M. Abdul Hussain, & Habbi, H. M. D. , “11. Maximum Power Point Tracking Photovoltaic Fed Pumping System Based on PI Controller. 2018 Third Scientific Conference of Electrical Engineering (SCEE), 78–83. https://doi.org/10.1109/SCEE.2018.8684120,” 2018.
[11] R. K. Varma, & Akbari, M. , “Simultaneous Fast Frequency Control and Power Oscillation Damping by Utilizing PV Solar System as PV-STATCOM. https://doi.org/10.1109/TSTE.2019.2892943,” IEEE Transactions on Sustainable Energy, vol. 11, no. 1, pp. 415–425, 2020.
[12] D. Rimorov, Joos, G., & Kamwa, I. , “Design and implementation of combined frequency/oscillation damping controller for type 4 wind turbines., https://doi.org/10.1109/PSCC.2016.7540909,” 2016 Power Systems Computation Conference (PSCC), pp. 1–7., 2016.
[13] M. Yang, Cui, Y., & Wang, J., “Multi-Objective optimal scheduling of island microgrids considering the uncertainty of renewable energy output. https://doi.org/10.1016/j.ijepes.2022.108619,” International Journal of Electrical Power & Energy Systems, vol. 144, 2023.
[14] M. M. A. Awan, Javed, M. Y., Asghar, A. B., & Ejsmont, K., ” Performance Optimization of a Ten Check MPPT Algorithm for an Off-Grid Solar Photovoltaic System,https://doi.org/10.3390/en15062104,” Energies, vol. 15, no. 6, p. 2104, 2022, doi: https://doi.org/10.3390/en15062104.
[15] P. P. Kulkarni*, & Deshmukh, S. P. , “Different Converter Topologies for Solar Photovoltaic System with methods for Maximum Power Point Tracking Algorithms. , . https://doi.org/10.35940/ijitee.J1202.0981119,” International Journal of Innovative Technology and Exploring Engineering, vol. 8, no. 11, pp. 1112–1118, 2019.
[16] J. E. Mendoza, López, M. E., Fingerhuth, S. C., Peña, H. E., & Salinas, C. A., “15. Low voltage distribution planning considering micro distributed generation..https://doi.org/10.1016/j.epsr.2013.05.020,” Electric Power Systems Research,, vol. 103, pp. 233–240, 2013.
[17] A. Q. Al-Shetwi, Issa, W. K., Aqeil, R. F., Ustun, T. S., Al-Masri, H. M. K., Alzaareer, K., Abdolrasol, M. G. M., & Abdullah, M. A. , ” Active Power Control to Mitigate Frequency Deviations in Large-Scale Grid-Connected PV System Using Grid-Forming Single-Stage Inverters https://doi.org/10.3390/en15062035,” Energies, vol. 15, no. 6, p. 2035, 2022, doi: https://doi.org/10.3390/en15062035.
[18] K. Liao, Xu, Y., Yin, M., & Chen, Z., ” A Virtual Filter Approach for Wind Energy Conversion Systems for Mitigating Power System Frequency Fluctuations . https://doi.org/10.1109/TSTE.2019.2922302,” IEEE Transactions on Sustainable Energy, vol. 11, no. 3, pp. 1268–1277, 2020.
[19] R. Rajan, Fernandez, F. M., & Yang, Y., ” Primary frequency control techniques for large-scale PV-integrated power systems: A review.https://doi.org/10.1016/j.rser.2021.110998,” Renewable and Sustainable Energy Reviews,, vol. 144, 2021.
[20] Q. Zhang, Xie, J., Pan, X., Zhang, L., & Fu, D. , “A Short-Term Optimal Scheduling Model for Wind-Solar-Hydro-Thermal Complementary Generation System Considering Dynamic Frequency Response. https://doi.org/10.1109/ACCESS.2021.3119924,” IEEE Access, vol. 9, pp. 142768–142781., 2021.
[21] M. M. Mohamed, el Zoghby, H. M., Sharaf, S. M., & Mosa, M. A., “Optimal virtual synchronous generator control of battery/supercapacitor hybrid energy storage system for frequency response enhancement of photovoltaic/diesel microgrid.https://doi.org/10.1016/j.est.2022.104317,” Journal of Energy Storage, , vol. 51, 2022.
[22] V. D. Paduani, Yu, H., Xu, B., & Lu, N., “A Unified PowerSetpoint Tracking Algorithm for Utility-Scale PV Systems With Power Reserves and Fast Frequency Response Capabilities, https://doi.org/10.1109/TSTE.2021.3117688,” IEEE Transactions on Sustainable Energy, vol. 13, no. 1, pp. 479–490., 2022.
[23] K. Saadaoui, Rhazi, K. S., Mejdoub, Y., & Aboudou, A. , “Modelling and simulation for energy management of a hybrid microgrid with droop controller, https://doi.org/10.11591/ijece.v13i3.pp2440-2448,” International Journal of Electrical and Computer Engineering (IJECE), , vol.13, no. 3, p. 2440, 2023.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 99 NR 12/2023. doi:10.15199/48.2023.12.07