Published by 1. Tomasz PERZYŃSKI1, 2. Vitaliy LEVONIUK2, 3. Radosław FIGURA1, Faculty of Transport, Electrical Engineering and Computer Science, University of Technology and Humanities in Radom (1) Department of Electrical Systems, Lviv National Agrarian University (2)
ORCID: 1. 0000-0001-5105-5034; 2. 0000-0003-2113-107X; 3. 0000-0001-8048-5623
Abstract. The mathematical model of a fragment of ultrahigh voltage electric network is developed in this paper. The network consists of a long power line with distributed parameters and equivalent three-phase active-inductive load. Transient electromagnetic processes are analysed in present work. The results of transient electromagnetic processes simulation in the form of analysed figures are shown. All the results presented in this paper were obtained exclusively using numerical methods.
Streszczenie. W pracy zaprezentowano model matematyczny fragmentu sieci elektroenergetycznej wysokiego napięcia. Sieć składa się z długiej linii elektroenergetycznej o rozłożonych parametrach i równoważnym trójfazowym obciążeniu czynno-indukcyjnym. W niniejszej pracy analizowane są przejściowe procesy elektromagnetyczne. Przedstawiono wyniki symulacji nieustalonych procesów elektromagnetycznych w postaci wykresów. Wszystkie wyniki przedstawione w niniejszej pracy uzyskano wyłącznie metodami numerycznymi. (Analiza przejściowych procesów elektromagnetycznych w linii przesyłowej wysokiego napięcia podczas zwarć dwufazowych).
Słowa kluczowe: elektromagnetyczne procesy przejściowe, warunki brzegowe, zwarcie dwufazowe, sieć elektroenergetyczna.
Keywords: transient electromagnetic processes, boundary conditions, short circuit, electrical network.
Introduction
It is necessary to take into consideration the occurrence of emergency modes when designing electrical networks. It is important to do as they usually are accompanied by damage to the elements of electrical networks. The most dangerous and common emergency mode is a short circuit mode. After all, there are significant short-circuit currents in the elements of electrical networks. They cause thermal and electrodynamic action and are accompanied by a sharp voltage decrease in the electrical network. Short-circuit currents can overheat conductive parts or even melt wires (temperatures can reach up to 20000 °K). So there comes a partial or complete termination of electricity supply to consumers. Also, this damage leads to damage caused by an electric arc that occurs at the point of short circuit and can affect adjacent objects.
Short circuits decrease the voltage at the network nodes which affects the technological processes disruption and the stability of the power system as well. Analysis of recent research A mathematical models for the calculation of electromagnetic transient processes are included in the [1- 5]. The model in three-phase lines has been developed in [6]. But the model can be used at two-phase short circuits as well.
Analysis of recent research
Paper [7,8] presents a mathematical model of the transmission line, which is based on the methods of “lost elements” and “space state of the line”. The proposed method is a simple and practical procedure for modeling the three-phase transmission line directly in the time domain without explicitly using inverse transforms. Satisfactory verification of the obtained results with the performance of the EMTP-RV software suite has been presented.
In [9–11], a mathematical model of a power transmission line with distributed parameters was created, which is based on the equations of a long line of the first order with given boundary conditions of voltage and current along the edges of the line.
In [12], the application of first-order long-line equations for the study of transients processes in the ground wire is considered. The simulation is performed in the frequency domain with the subsequent transition to time.
The article [13] presents a mathematical model of a perfectly transposed three-phase power line. The model allows you to calculate phase currents and voltages along the line as a function of time coordinate. An analysis of the results of a computer simulation that turns on the power line in non-working stroke mode is presented in the paper.
A model of three-phase power lines with distributed parameters has been created in [14] using the software package PSCAD. This model can be used to simulate transient electromagnetic processes during switching, short circuits and other modes of line operation.
In [15] the study of overvoltages in the line of ultrahigh voltage was carried out. The power line here is represented by a series connection of alternate circuit circuits. The computer simulation was performed in the ATP software package.
In [16], with the help of the PSCAD software package, surge simulations in the 500 kV line during a lightning strike were simulated. The coronation phenomenon of wires was neglected during the simulation, ie the running phase and interphase active conductivities were not taken into account.
For the analysis of transient processes in a three-phase power line with arbitrary voltage and current distributions in the line, it is proposed to use the numerical inverse Laplace transform algorithm in [17]. Here the Laplace transform methodology is also used to find voltages and currents along the line edges. Phase voltages and currents are obtained as rational functions of their frequency. It is shown how the numerical inverse Laplace transform can be applied to obtain the distribution of electromagnetic waves in a power line.
The transient electromagnetic processes in symmetric and asymmetric short circuits in different places of the high-voltage power line connected to the generating unit busbars. They are analysed in [18]. The equations of voltages and currents of the transmission line and substation buses are written in phase coordinates. It gives a possibility to model easily different asymmetric states. Here, a model for the transient electromagnetic processes analysis has been developed in the MatLab/Simulink software package.
Analysis of the available literature has shown that most studies of transient electromagnetic processes in power lines are carried out by replacing the equation of the long line (telegraph equation) with a circular equivalent [13-16], which is not always effective. Also, we can say that to the mathematical modelling of these processes in long power lines at the field level is given insufficient attention. It is a fact, that work in this direction has been underway for a long time. Commonly used approaches require well-defined boundary conditions to the long line equation [6, 9, 12, 17], or they are burdened by analytical integration [7,8]. With regard to the MatLab/Simulink software package, the distributed parameter line model built into the Simulink library is simplified. This model doesn’t take into account the running resistance, phase and interfacial conductivity, in order to simplify the calculations by the method of D’Alembert [18-20]. The same approaches are used in other software tools [21]. But this may affect the adequacy of the results.
Thus, the aim of the work is to develop methods of mathematical modelling and analysis of transient electromagnetic processes in long three-phase power lines in emergency modes.
Presentation of basic material
To obtain equations of the electromagnetic state of the studied objects, researchers usually use two main approaches. The first is a classical approach based on the law of conservation of energy. The second is a variational approach based on minimizing the functionality of the studied object. Each of these approaches has its drawbacks and advantages, but when used correctly, they both lead to the right results [22].
We propose to use a modified Hamilton–Ostrogradsky principle (variational approach) for the analysis of transient electromagnetic processes in the elements of electrical networks [23]. This approach avoids the decomposition of a single dynamic system. The initial equations of the electromagnetic state of the object under study can be obtained solely on the basis of a single energy approach by constructing an extended Lagrange function [23]. This approach is especially relevant for systems with distributed parameters, in particular for long power lines.
The theory of transient electromagnetic processes analysis in long power lines based on variational approaches in a single-line version was developed in [23] and further developed in [24]. To reproduce fully these processes in long power lines, which often operate in asymmetric modes, they are necessary to be modelled in multiphase execution. Therefore, we will build a mathematical model of the line in three-phase execution.
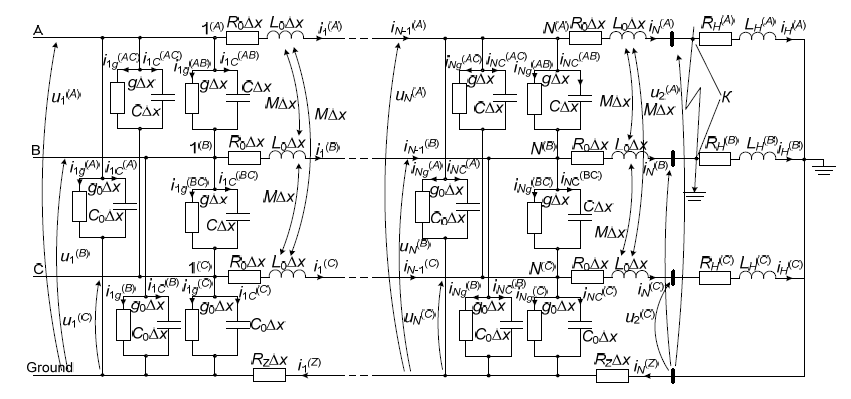
Fig. 1 presents the calculation scheme of the electrical network fragment we study. The key element is a long power line. It is presented in three-phase design as a line with distributed parameters (here are shown only the first and last discrete nodes of the line). A voltage is applied to the beginning of the line. At the end an equivalent three-phase active-inductive load is connected to it.
There are elements both with the concentrated and with the distributed parameters in the fragment of an electric network we investigated.
Hamilton-Ostrogradsky principle
Therefore, the Hamilton-Ostrogradsky action functional looks like this [23]:

where S – action according to Hamilton–Ostrogradsky; I – energy functional; L* – extended Lagrange function, Ll – linear density of the modified Lagrange function [23]:
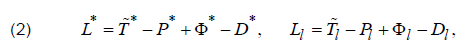
where T~* – kinetic coenergy, P* – potential energy, Φ* – energy dissipation, D* – energy of outside nonpotential forces, with index l the corresponding linear densities of energies.
It is possible to get acquainted with a technique of receiving similar equations of an electromagnetic state. For example, in our works [25-27]. Therefore, in order to reduce the volume of material, we propose ready-made equations for the studied fragment of the electrical network (Fig. 1).
Mathematical model of a fragment of the electric network
We present the final equations of the electromagnetic state of the studied fragment of the electrical network in matrix-vector form:


In (3) and (4) L0, R0, C0, G0 – inductance, resistance, capacitance and conductivity matrix.
The problem of solving (3) is to determine the boundary conditions. In our case we know the voltage at the beginning of the line (u1 = u│х = 0), but not at the end of it. Therefore, it is necessary to find only the boundary condition at the end of the line. Note that the line is loaded with an equivalent three-phase active-inductive load.
In [24] symmetrical modes were considered for homogeneous long power lines. That is why the line was modelled in a single-phase (single-line) design. We propose to use the boundary conditions of the second and third genera (boundary Neumann and Robin–Poincare conditions). Also the equation that can be obtained by Kirchhoff’s second law for electric circuits with distributed parameters. We propose to use this approach for three-phase systems. Let’s write the mentioned equation in matrix-vector form:

By discretizing (1) by the method of lines, using the notion of the central de-rivative, we obtain:

Write (6) and (7) for the last discrete node of the line (j = N):
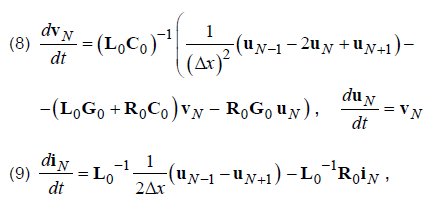
Analysing (8) and (9), we see that they have an unknown voltage in the fictitious node uN+1. This makes it impossible to find the voltage at the last discrete node of the line uN (8). Also we cannot find the current in the last discrete branch of the line іN (9). The voltage uN+1 does not exist in nature and it has no physical meaning. It is a purely fictitious-mathematical quantity.
The value of the current in the first discrete branch of the line or, if necessary, in all discrete line branches, can be calculated by discretizing (5) by the lines method, but now using the concept of the right derivative:

Computer simulation results
We wrote program code in the algorithmic programming language Visual Fortran to perform a computer simulation, based on the developed mathematical model. The code allows you to reproduce transient electromagnetic processes in the studied fragment of the electrical network (Fig. 1).
Description of the order and parameters of the simulation
The simulation was performed as follows in the first experiment. The power line was switched on at time t = 0s with asymmetric equivalent three-phase active-inductive load on the normal mode of operation. A two-phase short circuit to ground was simulated after entering the steady state, at time t = 0,11s, at the end of the power line (phases A and B, see Fig. 1).
The power line in the second experiment was switched on for a two-phase short circuit at the end of the power line at time t = 0s (as in the previous experiment, the short circuit to ground was simulated in phases A and B).
Experiment
Fig. 2 show the spatial distributions of phase voltages at time t = 0,001s and phase currents at time t = 0,007 s, respectively. These figures reflect very well the course of wave electromagnetic processes in the power line, so let’s analyse them.
We can see from Fig. 2 that during the start of the transmission line to normal operation at time t = 0,001s, the voltage of phase A at the beginning of the line has a value of 200 kV. At a distance of 350 km from the beginning of the line, the voltage is still zero.

Figure 3 show the temporal-space voltage and current distributions of phase B. These figures are made in 3D format, they combine both time and space distributions of voltage and current in a line.
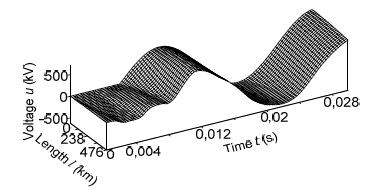
The analyse of the mentioned figures show that when the line is switched on for an equivalent asymmetric active-inductive load. The phase B voltage has the largest fluctuations at the end of the power line (Fig. 3).
It is advisable to analyze Fig. 3 together with Fig. 2.
Conclusion
The application of Neumann and Robin–Poincare boundary conditions to identify boundary conditions to the differential equation of a long line of the second order makes it possible to effectively solve problems related to the analysis of transient electromagnetic processes in ultrahigh voltage lines, where they must be considered as distributed parameters.
Introduction to the mathematical model of the line, which is based on a discretized equation of a long line. To solve it the boundary conditions of the second and third genera are applied, the parameter “output voltage” (voltage at the end of line u2) allows making the line model more autonomous and universal on the one hand. On the other – opens wider possibilities for reproduction of emergency states of operation of the line.
Presented in 3D format temporal-spatial distributions of voltages and currents maximally illuminate information about wave processes in the line. They also confirm the physical principles of electrodynamics regarding the flow of wave electromagnetic processes in long power lines. They indicate the high adequacy of the developed mathematical model.
The materials of this work will be used in further research on the joint operation of turbogenerators, unit transformers, switching facilities and ultra-high voltage long transmission lines.
LITERATURE
[1] Szafraniec, A., Halko, S., Miroshnyk, O., Zharkov, A., Vershkov, O., Magnetic field parameters mathematical modelling of windelectric heater, Przeglad Elektrotechniczny, 97(8) (2021)
[2] Czaban, A., Levoniuk, V., Figura, R., The mathematical model of high voltage switch as an element of a power system, Przeglad Elektrotechniczny, 97(7), 94-97, (2021)
[3] Lis M., Chaban A., Szafraniec A., Levoniuk V., Figura R., Mathematical modelling of transient electromagnetic processes in a power grid, Przegląd Elektrotechniczny, nr 12/2019, 160-163
[4] Chaban, A., Perzyński, T., Popenda, A., Figura, R., Levoniuk, V., Mathematical Modeling of Transient Processes in the Susceptible Motion Transmission in a Ship Propulsion System Containing a Shaft Synchronous Generator, Energies, 15(9), (2022), 3266
[5] Popenda A., Szafraniec A., Chaban A., Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation, Energies, 14 (2021), 7882
[6] Lobodzinsky V., Chibelis V., Mathematical model of a threephase line with distributed parameters in electromagnetic transients, BULLETIN OF KNUTD, (2018), No. 4, 96-102
[7] Costa E.C.M., Kurokawa S., Pissolato J., Prado A.J., Efficient procedure to evaluate electromagnetic transients on threephase transmission lines, IET Generation Transmission & Distribution, (2010), No. 4, 1069-1081
[8] Colqui J.S.L., de Ara´ujo A.R.J., Kurokawa S., Performance of the modified lumped parameter model in the electromagnetic transient analysis, Proc. the 13th latini-american congress on electricity generation and transmission, (2019)
[9] Andrade L., Leite H., Leao M., Time-domain distributed parameters transmission line model for transient analysis, Progress In Electromagnetics Research B., 53 (2013), 25-46
[10] Chaban A., Lis M., Szafraniec A., Chrzan M., Levoniuk V., Interdisciplinary modelling of transient processes in local electric power systems including long supply lines of distributed parameters, IEEE Xplore, 2018 Applications of Electromagnetics in Modern Techniques and Medicine (PTZE), 17–20
[11] Czaban A., Lis M., Szafraniec A., Chrzan M., Levoniuk V., Analysis of transient processes in a power supply system of concentrated and distributed parameters based on variational approaches, Przegląd Elektrotechniczny, 94 (2018), nr 12, 154-157
[12] Shi Z., Liu L., Xiao P., Geng Z., Fang G., Applying transmission line theory to study the transmitting turn-off current in a long grounded wire, IEEE Transactions on Antennas and Propagation, 65 (2017), No. 10, 5112-5122
[13] Kizilcay M., Teichmann K., Papenheim S., Malicki P., Analysis of switching transients of an EHV transmission line consisting of mixed power cable and overhead line sections, Proc. International Conference on Power Systems Transients, (2017)
[14] Smolarczyk A., Chmielak W., PSCAD / EMTDC as a convenient tool for modeling overhead lines, Works of the electrotechnical institute, (2016), No. 272, 31-48
[15] Nuricumbo-Guillén R., Espino Cortés F.P., Gómez P.,. Martínez C.T, Computation of transient profiles along nonuniform transmission lines including time-varying and nonlinear elements using the numerical Laplace transform, Energies, (2019), No. 12, 3227
[16] Chen C., Han Y., Liu J., Mo W., Yuan Z., Huang J., Su H., Zhang X., Wu K., Research on the lightning intruding overvoltage and protection measures of 500 kV AC fault current limiter, Energies, (2019), No. 12, 3845
[17] Jung-Chien Li, Transient analysis of three-phase transmission lines with initial voltage and current distributions, Electric power systems research, 35 (1995), No. 3, 177-186
[18] Pruski P., Paszek S., Analysis of transient waveforms in a power system at asymmetrical short-circuits, Przeglad elektrotechniczny, (2020), No. 2, 26-29
[19] Vijaya T.С., Nandhini M., Sundar R., Nithiyanantha K., MATLAB based simulations model for three phases power system network, International Journal for Research in Applied Science & Engineering Technology, 4 (2016), No. 11, 502-509
[20] Shcherba A., Podoltsev A., Kucheryavaya I., Electromagnetic processes in a cable line with polyethylene insulation at a voltage of 30 kV, Technical electrodynamics, (2013), No. 1, 9-15
[21] Rout B., Pati B.B., MFO Ptimized Fractional Order Based Controller on Power System Stability, Proceedings of Engineering and Technology Innovation, 8 (2018), 46-59
[22] White D.C., Woodson H.H., Electromagnetic energy conversion, New York: John Wiley & Sons Inc., (1958)
[23] Chaban A., Principle Gamіltona-Ostrogradskogo in elektromechanіcal systems, Lviv: T. Soroky, (2015)
[24] Levoniuk V.R., Methods and means of analysis of switching transients processes in ultra high voltage transmission lines on the basis of variational approaches, Ph.D. dissertation, Department of Electrical Systems, Lviv Nat. Agrarian Univ., Lviv, Ukraine, (2019)
[25] Czaban A., Szafraniec A., Levoniuk V., Mathematical modelling of transient processes in power systems considering effect of high-voltage circuit breakers, Przeglad Elektrotechniczny, (2019), No. 1, 49-52
[26] Chaban A., Levoniuk V., Drobot I., Herman A., Mathematical model of electromagnetic processes in Lehera line at opencircuit operation, Electrical engineering & electromechanics, (2016), No. 3, 30-35
[27] Chaban A., Lis M., Szafraniec A., Levoniuk V., Mathematical Modelling of Transient Processes in a Three Phase Electric Power System for a Single Phase Short-Circuit, Energies (2022), No, 15, 1126
Autorzy: dr hab. inż. Tomasz Perzyński, prof. UTH Rad., University of Technology and Humanities in Radom, Faculty of Transport and Electrical Engineering, ul. Malczewskiego 29, 26-600 Radom, Email: t.perzynski@uthrad.pl; Ph.D. Vitaliy Levoniyk, Lviv National Agrarian University, Department of Electrical Systems, 1, V. Velykogo str., 80381 Dubliany, Lviv region, Ukraine, E-mail: Bacha1991@ukr.net; dr inż. Radosław Figura, University of Technology and Humanities in Radom, Faculty of Transport and Electrical Engineering, ul. Malczewskiego 29, 26-600 Radom, Email: r.figura@uthrad.pl.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 98 NR 12/2022. doi:10.15199/48.2022.12.67