Published by Sergey CHIZHMA, Artyom ZAKHAROV, Immanuel Kant Baltic Federal University (Kaliningrad, Russia)
Abstract. The authors explore a number of methods of calculating insolation on a tilted arbitrarily oriented surface and choose the most efficient one for conducting the performance and efficiency analysis of solar power plants. The validity of the method is tested using the statistical data of the Kaliningrad region. The authors describe an algorithm for calculating insolation in the Matlab software programme, based on the following data: the position of the Sun, the average monthly climatic characteristics of the region, beam, scattered and reflected insolation as well as the proportion of these types of insolation on a tilted surface. The authors validate the results of their calculations by comparing them with statistical averages.
Streszczenie. Analizowano metody obliczania nasłonecznienia dowolnie pochylonej powierzchni. Walidację metody przeprowadzono na podstawie danych statystycznych regionu Kaliningrad. Obliczenia przeprowadzono na podstawie znajomości pozycji słońca, średniej miesięćżnej informacji klimatycznej, średniego nasłonecznienia. (Metoda obliczania nasłonecznienia dowolnie pochylonej powierzchni)
Keywords: alternative energy, insolation, energy, efficiency
Słowa kluczowe: energia nasłonecznienia, ogniwa fotowoltaiczne
Introduction
The construction of solar power plants requires assessment of energy potential of a chosen territory. In most cases, design solutions for solar power plants are based on long-term average measurements that include the average daily solar energy (kWh/(m2·day)), average daily wind speed (m/s), etc. The main sources of data used for estimating solar energy potential are insolation maps, NASA data [1] and the data provided by the World Radiation Data Centre [2] for actinometric stations of the World Meteorological Organization (WMO) network, etc. [3]. There is an extensive body of literature on hybrid energy solutions, types of renewable energy, their classification and composition. Reviews on different types of solar energy solutions are presented in [4-6].
There is a need for a more accurate assessment of the efficiency of solar power plants. This task requires more objective data reflecting the impact of a number of factors associated with the location and the position of solar panels, annual variations in the length of daylight hours, and cloudiness. In our research, we propose to move from the average energy parameters, which are, in essence, quantitative characteristics of insolation, to instantaneous values of insolation incident on a tilted surface in order to determine daily fluctuations of insolation. We also propose a method for assessing the efficiency and performance of solar power plants based on this approach.
The aim of the research
The main aim of our research is to test a method of calculating insolation for obtaining more accurate data on its instantaneous values based on geographical location and average climatic parameters. We hold that the obtained data can be used for modeling and assessing the energy generation performance of solar power plants [7] and the optimization of their control algorithms. We tested the proposed method using input data for the Kaliningrad region and validated the results of the calculation.
To achieve the aim, we analysed a number of calculation methods, which are based on the algorithm for determining the position of the Sun for different geographic locations and seasons (Section 1). Various computational methods for estimating insolation on the Earth’s surface are described in the works of Liu and Jordan [8-10], KolaresPereira and Rabl [11], and Gueymard [12-13].
We have chosen one calculation method that meets the objectives of our research (See Section 2) and used it for the determination of solar insolation on a tilted surface (Section 3). The selected model has been applied to obtain insolation data for the Kaliningrad region for one year. Power plants based on renewable energy sources can be simulated with obtained data, as shown in [14-15]. The results of our calculations have been verified (Section 4).
1. Methods of calculating the position of the Sun
The existing methods of estimating instantaneous values of insolation require the analysis of the position of the Sun above the Earth’s surface [16]. The annual change in solar activity is associated with two main factors: the annual change in the solar declination angle δs, and the annual change in the distance between the Earth and the Sun. The axial tilt of the Earth’s orbit is 23.45°. Thus, the declination angle δs (solar declination) varies in the range from -23.45° to 23.45° during the year and can be calculated using the Cooper formula [17]:

where n is the ordinal number of the day in the year.
To simplify the calculation of the position of the Sun above the Earth’s surface, the Earth is considered as a stationary object. Figure 1 shows that the observation point is assumed as the origin of the coordinates. In this system, the Sun is a moving object and rotates around the centre of the Earth with an angular velocity of 15° per hour. The zenith point (or local noon) is taken as the starting point for the revolution of the Sun. The value characterizing the movement of the Sun around the Earth is called the solar hour angle hS. It is calculated using the formula:

The two values, the angular height of the Sun α and the azimuth angle of the Sun αs are used to calculate the spherical coordinates of the position of the Sun above the Earth’s surface:

where L is the geographical latitude.

Solar radiation on the Earth’s surface depends on the changes in the distance between the Earth and the Sun during the year: on the day of the winter solstice, December 21, it is 1,471·1011 m and on the day of the summer solstice, June 21, it constitutes 1,521·1011 m. This variability is a function of the elliptical shape of the Earth’s orbit, which is taken into account when translating the so-called solar time (the zenith time is 12.00) into local time using the following formula:

where ET is the equation of time, taking into account the variability of the Earth’s rotation speed around the Sun, lst is the standard time meridian, llocal is the local longitude. ET is determined using the formula given below:

2. The analysis of the methods of calculating insolation on the Earth’s surface
The calculation of insolation on the surface of the Earth is a difficult task since it requires taking into account a variety of factors. There are many empirical or semiempirical approaches to the problem within which a number of simplifying assumptions are made. Each of the assumptions is based on the calculation of three main types of insolation on the Earth’s surface: beam insolation (Ib.c), scattered or diffused insolation (Id.c) and reflected insolation (Ir.c):

To account for the absorbing effect of clouds, a monthly clearness index (KT) is introduced. It can be calculated using the formula:

where Hh [kWh/(m2·day)] is the monthly average daily radiation on a horizontal surface, and Ho.h [kWh/(m2·day)] is the monthly average daily extraterrestrial radiation [16].
This index was first proposed in the works of Liu and Jordan [8–10]. The method of calculating radiation, considered in the framework of this approach, is applied to monthly average values. In our research, we propose to calculate the instantaneous values of insolation during the day. There are a number of methods that allow researchers to move from average values of solar radiation to instantaneous ones:
• the Kolares-Pereira and Rabla method developed in 1979 (CPR-method) [11],
• the Kolares-Pereira and Rabla method, modified by Gyeumard in 1986 (CPRG-method) [12],
• the Daily Integration (DI) Model, developed by Gyeumard in 2000 [13].
Based on the data presented by Christian A. Gueymard in [13], the daily integration (DI) model is more accurate than other methods listed above. Therefore, in this paper, the calculation of insolation is done using this method. The daily integration model is based on the calculation of rd and rt, which change during daylight hours. They demonstrate the dependence of instantaneous diffused insolation and instantaneous insolation on a horizontal surface on the total daily scattered insolation and total daily insolation on a horizontal surface, respectively.
The coefficient rd is defined as follows:

where hss is the solar light angle corresponding to the sunset, hereinafter expressed in radians. The method of calculating hss is described in [16].
According to the daily integration model, the rt coefficient is calculated as follows:
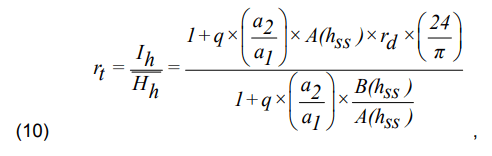
where the absorption of radiation in the atmosphere is taken into account using the ratio a2/a1:
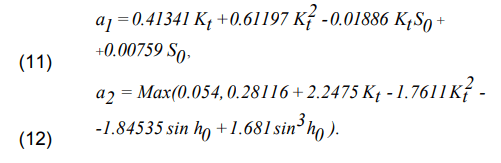
The coefficients A(hss) and B(hss) are defined as follows:

Missing values for the calculation are defined as indicated below:

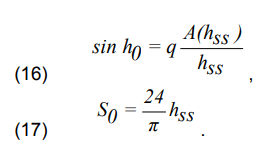
Thus, the instantaneous value of insolation on the horizontal surface Ih [Wh/m2] and the instantaneous value of diffused insolation Id [Wh/m2] can be calculated in the following way:

Then, beam insolation on a horizontal surface, Id.h [Wh/m2] is calculated according to the formula:

3. Calculation of solar radiation on a tilted surface
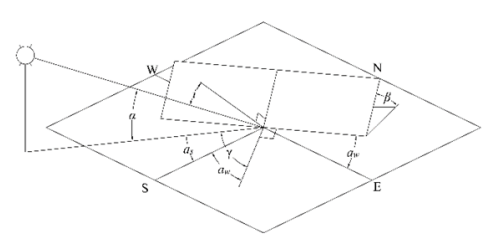
The values of insolation obtained using the daily integration method are to be converted into insolation values for solar panels oriented and tilted in a particular way. The position of solar panels is set at the following angles (Fig. 2): the tilt of the solar panels β and the azimuth angle of the solar panels αw. The incident angle of sunlight on the surface of the solar panels i is determined as follows:

Using simple transformations, we determine the fraction of beam insolation on the tilted surface Ib.c:

Scattered insolation (Id.c) on the surface of solar panels is estimated as follows:

Reflected insolation (Ir.c) is calculated using the formula:
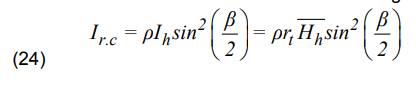
where ρ = 0.2 for the surface not covered with snow, and 0.8 for the snow-covered surface.
Thus, the insolation on the tilted surface is determined as follows:
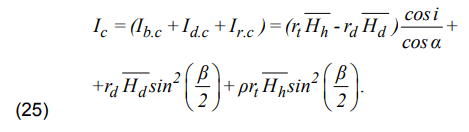
4. Calculation of insolation for the Kaliningrad region
The calculation method described in the sections above was used in the MATLAB software programme for obtaining the annual insolation data for the Kaliningrad region (54°43′N, 20°30′E). The algorithm (Fig. 3) is based on NASA resource data [1], where Hh is average monthly total radiation on a horizontal surface per day, Hd is average monthly total scattered radiation, and KT is monthly clearness index:

Other input data for the algorithm are the latitude, the longitude of the chosen terrain, the start and finish dates of the formation of the calculated insolation values, as well as parameters characterising the location of the solar panels. The algorithm performs the calculation of the ordinal numbers of the days in the year (taking into account leap years) for which the calculation of solar insolation is done. NASA data are monthly averaged, so before starting the calculation, the change in monthly average indicators is interpolated, and their values for each day are determined. The variable, linearly dependent on time, is the hour angle of the Sun hs, for which every minute values are calculated. After all the data have been formed, the MATLAB software programme calculates the total insolation on a tilted surface, thus forming the data array Ic.
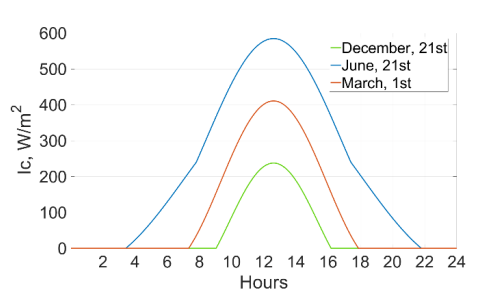
Figure 4 shows the calculated insolation on the surface of a solar panel having a 30° tilt angle on December 21, June 21, and March 1.
The reliability of the calculation method and the data obtained have been assessed. To perform the assessment we analysed the calculated total monthly radiation incident on a horizontal as well as on a tilted surface. The results are shown in Fig. 5, where Hh.calcu is the calculated average monthly total radiation, Hh is the average monthly total radiation according to NASA [1], and Hc is the monthly average total radiation.
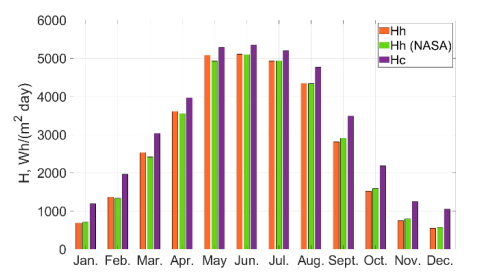
The graph shows that the margin of error of the proposed method is minimal. It allows us to use the obtained data for the performance and efficiency analysis of solar power plants.
Conclusions
In our research, a number of methods for calculating instantaneous values of insolation have been analysed. The methods are based on the calculation of the coordinates of the position of the Sun (the angular height and the azimuth angle), as well as the average climatic parameters of the season.
Our analysis of the calculation methods has shown that the daily integration model (DI) is the most effective one. On the basis of this model, we proposed an algorithm for calculating insolation using the MATLAB software programme. This allowed us to determine instantaneous values of insolation for a wide variety of temporal and geographic conditions. The algorithm can be used to form an array of objective data on the instantaneous values of insolation on the tilted surface of solar panels, as a combination of beam, diffused and reflected insolation.
We validated the obtained data and identified the margin of error of the proposed method, which turned out to be insignificant. The proposed method of calculation can be used to simulate the operation of power plants working on renewable energy sources, evaluate their efficiency and to conduct further research on optimizing control algorithms for autonomous solar power plants.
REFERENCES
[1] https://power.larc.nasa.gov/data-access-viewer/.
[2] World Radiation Data Centre. Available at: http://wrdc.mgo.rssi.ru/ (accessed 14 March 2017)
[3] Popel’ O.S., Frid S.E., Kiseleva S.V., Kolomiec Ju.G., Lisickaja N.V. Klimaticheskie dannye dlja vozobnovljaemoj jenergetiki Rossii (Baza klimaticheskih dannyh). M.: Izd-vo MFTI. 2012
[4] Chauhan A., Saini R.P. A review on Integrated Renewable Energy System based power generation for stand alone applications: Configurations, storage options, sizing methodologies and control // Renewable and Sustainable Energy Reviews. – 2014. –V. 38. – Р. 99–120.
[5] Shivarama K.K., Sathish K.K. A review on hybrid renewable energy systems // Renewable and Sustainable Energy Reviews. – 2015. – V. 52. – Р. 907–916.
[6] Badwawi R.A., Abusara M., Mallick T. A Review of Hybrid Solar PV and Wind Energy System // Smart Science. – 2015. – V. 3 (3). – Р. 127–138.
[7] Obuhov S.G., Plotnikov I.A. Imitacionnaja model’ rezhimov raboty avtonomnoj fotojelektricheskoj stancii s uchetom real’nyh uslovij jekspluatacii. Izvestija Tomskogo politehnicheskogo universiteta. Inzhiniring georesursov. 2017. T. 328. № 6. 38–51
[8] Liu, B.Y.H., R.C. Jordan. 1960. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 4: 1–19.
[9] Liu, B.Y.H., R.C. Jordan. 1961a. Daily insolation on surfaces titled toward the equator. Trans. ASHRAE 67: 526–541.
[10] Liu, B.Y.H., R.C. Jordan. 1961b. Daily insolation on surface tilted toward the equator. Trans. ASHRAE 3(10): 53–59
[11] Collares-Pereira M, Rabl A. The average distribution of solar radiation: Correlations between diffuse and hemispherical and between daily and hourly insolation values. Solar Energy 1979; 22: 155-164.
[12] Gueymard C. Monthly averages of the daily effective optical air mass and solar related angles for horizontal or inclined surfaces. J Solar Energy Eng Trans ASME, 1986
[13] Gueymard C. “Prediction and Performance Assessment of Mean Hourly Global Radiation” Solar Energy, Vol. 68, No. 3, 2000, pp. 285-303. doi:10.1016/S0038-092X(99)00070-5
[14] Mirosław Mazur , Janusz Partyka , Tomasz Marcewicz. Analysis of the use of a hybrid power system of renewable wind and photovoltaic energy in residential buildings. PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 92 NR 8/2016. 113-116.
[15] Kazimierz Buczek, Wiesława Malska, Sebastian Penar. Use of PSIM software for modelling a small solar power station. PRZEGLĄD ELEKTROTECHNICZNY, 08/2011 Page no. 42.
[16] D. Yogi Goswami. Principles of solar engineering. Third Edition. CRC Press. Taylor & Francis Group 2015.
[17] Duffie J.A., Beckman W.A. Solar Engineering of Thermal Processes. Hoboken, New Jersey, John Wiley & Sons, Inc., 2013.
Authors: Prof. Sergey N. Chizhma, the Institute of Physics, Mathematics and Information Technologies, Immanuel Kant Baltic Federal University, Kaliningrad Russia. E-mail: chisn@yandex.ru, Artyom Zakharov, PhD student, the Institute of Physics, Mathematics and Information Technologies, Immanuel Kant Baltic Federal University, Kaliningrad, Russia. E-mail: AIZakharov@kantiana.ru.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 96 NR 11/2020. doi:10.15199/48.2020.11.26