Publised by Oleh HOLOVKO1, Adam KONIECZKA2, Adam DĄBROWSKI3, Politechnika Poznańska, Wydział Automatyki, Robotyki i Elektrotechniki (1, 2, 3)
ORCID: 2. 0000-0002-0362-3006; 3. 0000-0002-9385-6080O
Abstract. This paper proposes a method for evaluating the efficiency of passive cooling systems of solar panels in a type of radiator using CFD simulations. The movement of air through the cooling system and the dependence of the thermal state of the radiator on its shape, wind speed, and ambient temperature were analyzed. A mathematical analysis was made that takes into account the average temperature drop of a solar panel connected to a ribbed heat sink. Experimental measurements of the temperature of the solar panel were performed.
Streszczenie. W artykule zaproponowano metodę oceny wydajności pasywnych układów chłodzenia paneli fotowoltaicznych bazujących na radiatorach z wykorzystaniem symulacji CFD. Przeanalizowano ruch powietrza w układzie chłodzącym oraz zależność temperatury radiatora od jego kształtu, prędkości wiatru i temperatury otoczenia. Przeprowadzono analizę matematyczną uwzględniającą spadek średniej temperatury panelu fotowoltaicznego połączonego z żebrowym radiatorem. Wykonano eksperymentalne pomiary temperatury panelu fotowoltaicznego. (Modelowanie systemów chłodzenia pasywnego paneli fotowoltaicznych).
Słowa kluczowe: panel solarny; wydajność paneli solarnych; radiator; symulacje CFD.
Keywords: solar panel; efficiency of solar panels; heat sink; CFD simulations.
1. Introduction
According to [1], an increase in the installed capacity of photovoltaics in Poland amounted in 2021 to 3.7 GW. Data from the end of the first quarter of 2022 indicates the installed power of 9.4 GW. The global success of the solar industry is due to many factors but reduction of the cost of the generated electricity is crucial: according to [2] (Fig. 1), the cost of solar energy over the past 10 years has fallen 7.5 times.

The second reason is versatility: from small housing systems to large enterprises. In addition, unlike fossil-fuel electricity generation, solar energy causes no environment damage.
The main task with the use of solar radiation is to increase the efficiency of solar panels. The efficiency of commonly used photovoltaic panels is between 17 and 24% [3]. Most commonly used solar cells use wavelength range of 250 to 1100 nm to generate electricity. The remaining radiation is reflected or absorbed by the cells as heat. The temperature of the solar panel is influenced by external climatic variables such as wind speed, humidity, atmospheric temperature and concentrated dust [4]. The heat emission from the roof surface also plays an important role. The absorbed heat may raise the panel temperature even up to 70‒80°C. The result is a significant decrease in the output power.
The amount of energy loss of photovoltaic modules as a result of overheating shall be determined during the production tests. The thermal power loss in different models of silicon-crystalline batteries (according to the manufacturers’ catalog data) is on average within the limits of 0.45 to 0.50%/°C. Thin-film (amorphous) solar panels are more resistant to temperatures. Their thermal loss performance is about 0.2–0.3%/°C [5]. A way to improve the performance of solar panels is to keep their temperature within the optimum range. This method will not only increase electricity generation but also extend the life of the modules, which currently stands at 25 years.
There are many ways to cool solar panels:
1) Active cooling is carried out by forced air or liquid in both the area of the panel itself and the heat exchangers installed on the panels [6]. Problems with the use of active systems are mainly related to: additional equipment, which, as a rule, is not agreed upon with the manufacturer and additional costs of calculations, installation, maintenance. When using liquid-cooled systems, there is a problem of maintaining the installation in the winter to avoid damage.
2) Passive methods include panel cooling using phase conversion materials, heat pipes and radiators: conventional and micro-channel heat exchangers, nanofluids, spectral filters, and thermoelectric, evaporative and radiation cooling [6].
The method of natural cooling has great potential, does not require energy supply and is reliable and simple. In [7], based on the modeling results, the area of an additional surface needed to compensate for the heating of a solar panel was calculated. The size of the additional surface area should be 5‒5.5 times the size of the solar cell. However, the performed calculations do not take the shape of the cooling surface and the relative direction of the wind into account.
According to [8‒11], the use of a passive cooling system in the form of a radiator (aluminum or copper fins mounted on the back of the solar panel) allows the average temperature of the solar panel to be reduced by 2 to 7°C, thus raise its efficiency by 2‒4%.
In [12, 13] the efficiency of a radiator with perforated ribs was considered, and in [14‒17], a study of inclined and complex-shaped ribs was carried out. Depending on the geometry of the structure and wind speed, the temperature of the solar panel decreases by 4‒12 degrees. It should be noted that the measurements and calculations in the mentioned works were carried out for specific locations of solar panels and cannot be applied to other places and conditions.
The degree of the temperature drop depends on the characteristics and location of the panel, stochastic climatic conditions, the design used and the material of the cooling system. In order to estimate the magnitude of the temperature drop of a photovoltaic panel achieved with a heat sink, a full detailed analysis of the airflow shall be carried out, taking the effect of gravity into account, the design of the heat sink, the position and orientation of the panel and other objects near the panel.
CFD (Computational Fluid Dynamics) method can be used for modeling active and passive cooling systems. This method needs numerical analysis to analyze and solve fluid flow problems. In papers [18–21] thermal analysis of the heat sink in the conditions of air convection was considered. In [19] the CFD simulation results were compared with experimental results. Heat transfer tests were carried out for various shapes of radiators (solid pin fins, perforated pin fins, solid flat plate, and perforated flat plate). The achieved results show that the base temperature for experiment is typically 6.05% to 9.52% higher than the base temperature of the CFD simulation. Therefore, the use of CFD software for modeling parameters of heat transfer in passive cooling of solar panels in real conditions can be reasonable.
Section 2 presents the methodology for estimating and theoretical calculations of the temperature drop of a solar panel with a passive cooling system depending on the type of heat sink and external conditions (wind direction and speed). For this purpose the CFD modeling software Solidworks Flow Simulation was used. It allows for performing a simulation of fluid flow, advanced thermal analysis, and study of heat exchange between the designed components and the predefined medium.
Section 3 presents experimental verification of the temperature dependence of a photovoltaic panel without cooling and with a passive cooling system in the form of a rib radiator on external climatic conditions. A thermal imaging camera was used for experimental testing.
A brief summary and conclusions are provided in Section 4.
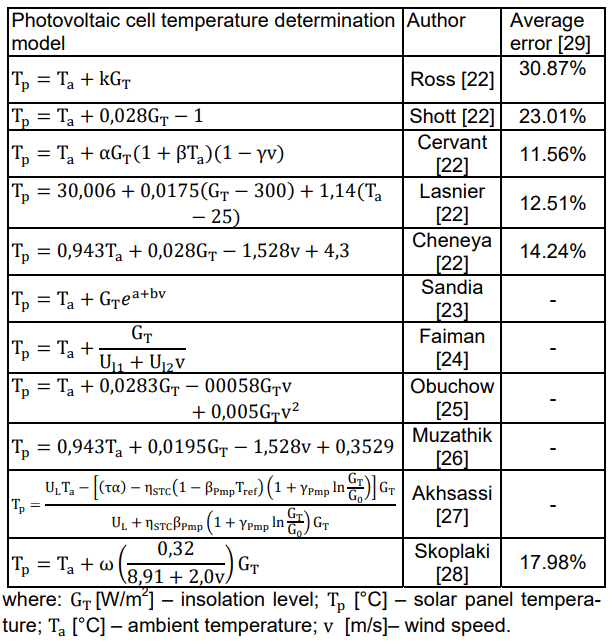
Table 1. Selected theoretical and statistical models to determine the temperature of a photovoltaic cell
2. Calculation of solar panel temperature and evaluation of effect of radiator shape on heat exchange efficiency
When calculating the temperature of the solar panel, the most influential factors are usually taken into account: the power of the solar radiation falling on the surface of the module, the ambient temperature and the wind speed. To determine the T୮ (temperature of the photovoltaic cell), various theoretical and statistical models have been proposed, determining the appearance, respectively [22‒28]. Table 1 shows commonly used T୮ calculation equations. However (according to [29]) depending on the chosen thermal model, the average error between the calculations and the measured value of the solar panel temperature can reach more than 30 percent.
The choice of a model and appropriate coefficients depends on the type of the panel and the conditions under which the panel is located. It can be determined from experimental data [30].
To analyze radiator performance, various ribbed radiators were modeled in Solidworks 3D CAD (2017), assuming that they are made of 5052-type aluminum alloy (thermal conductivity 140 W/mK (T=273K), density ‒ 2680 kg/m3 , specific heat ‒ 921 J/kg·K) [31].
During modeling, the following parameters were determined:
• P [W] ‒ total heat transfer capacity,
• Q [W/m2] ‒ the amount of heat distributed by the radiator surface unit,
• T [°C] ‒ initial temperature of the front surface of the heat sink,
• Tm [°C] ‒ average temperature of the heat sink,
• Tmin [°C] ‒ m
An example of the simulation obtained for a rib radiator is shown in Fig. 2.

Geometric dimensions of the heat sink affect the amount of dissipated heat. The purpose of the prepared tests is to perform a comparative analysis of heat exchange efficiency for the rib-type radiators with different rib heights ‒ L [mm].
Figure 3 summarizes the heat transfer efficiency of radiators of different shapes. The wind speed varied within 0‒ 20 m/s, the direction of air flow was perpendicular to the ribs at the rear, overheating of the front of the module in relation to the environment is 40°C.
Analysis of the dependence of the heat dissipation power on the surface of the radiator shows that under certain conditions the most efficient are radiators with a rib height of 20‒35 mm, providing a decrease in the module temperature on average from 5.74 to 11.8°C.
Compared to a flat plate of 5052-type aluminum alloy, the average heat dissipation power of the radiator increases 3.13 and 3.30 times, respectively. No further increase in the dimensions is recommended, since a significant part of the radiator does not participate in heat exchange with the environment.

Further tests shall aim to determine the optimum position of the radiator relative to the wind direction at different initial temperatures of the front panel.
Analysis of the heat dissipation efficiency of an unshielded radiator Q [W/m2] (Fig. 4) shows that the most efficient system is one in which the flows are directed perpendicular to the radiator from the ribs (100%) or along the ribs (99%). Changing the wind direction – from the front of the photo module (direction Z) or perpendicular to the ribs (direction X) – causes a decrease in efficiency by 55% and 40%, respectively.

The reason for such a decrease in the efficiency of the radiator as a cooling system is a significant decrease in wind speed in the area of the ribs. Figure 5 shows an example of the temperature distribution on the surface of the radiator and wind speed values in the radiator area.
In the next step, the dependences of the average temperature of the heat sink on the temperature difference between the heat sink and the surrounding air, wind speed and direction at the location of the panel were analyzed.
Figure 6 shows an illustrative calculation of the average heat sink temperature Tm[°C] for a radiator of dimensions 35×75×100 mm (s=0,063 m2) as a function of the initial temperature of the front surface T[°C] of the solar panel and wind speed. The influence of the thermal resistance between the solar panel and the radiator has not been taken into account.


The magnitude of the decrease in the average temperature of the radiator can be described using a mathematical function. Considering the above simulation, the decrease in the average temperature dTm[°C] at different temperatures T[°C] of the initial front surfaces can be described using the proposed mathematical expression
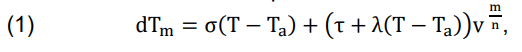
where σ, τ [°C ∙ s/m], λ[s/m] , m, n are determined using nonlinear regression of CFD simulation results.
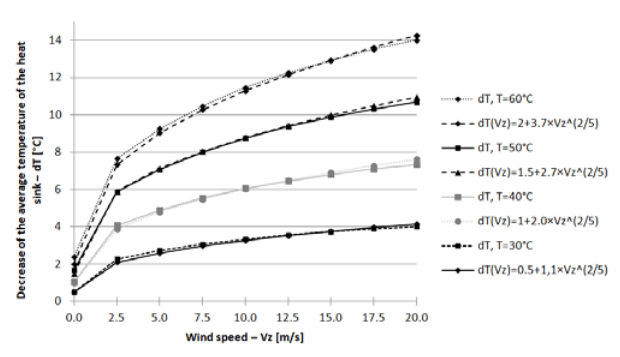
For example, when using a radiator with the rib thickness of 1 mm, the rib height of 35 mm, the distance between the ribs of 7.5 mm and the wind direction perpendicular to the radiator from the side of the ribs, the coefficients have the following values:

Figure 7 for a radiator (35×75×100 mm s=0.063 m2) shows the simulation dependence and proposed mathematical expression of the decrease in the average temperature of the dT[°C] on the wind speed, the temperature T[°C] of the initial front surface.
3. Experimental verification of the temperature dependence of a solar panel with passive cooling system on external climatic conditions
The Sandia thermal model [23] was used to calculate the theoretical temperature, which corresponds to experimental data for a SYP-S05V5W solar panel used in research [31].

The corresponding coefficients for a panel with a polymer substrate are: ε = 1 [K∙m2/W], a = -3.56, b = -0.075 s/m [23].
For an unshielded photovoltaic panel installed at an angle of 45°, taking into account the average wind direction in the Wielkopolska ‒ region south-west (at an angle of 45° at the rear of the solar panel), the coefficients in equation (1) (according to the next Solidworks Flow Simulation) determining the temperature decrease have the following values:
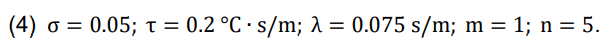
The use of an additional cooling module reduces the average temperature of the entire system (panel and heatsink). In this work a proportional dependence of the change in the average temperature of the solar panel with the cooling system on the temperature of the illuminated side it is assumed. This change can be recorded with a thermal imaging camera.
An experimental verification of the temperature dependence of a photovoltaic panel without heat sink and with a passive cooling system on external climatic conditions was carried out on 17th January 2022 in a place with coordinates 52.4028 and 16.9537 [31].
A radiator with dimensions of (35×75×100 mm) was vertically placed on the right hand side of the solar panel type SYP-S05V5w, the angle of inclination of the panel was 40°, the wind speed during the day varied within the limits (6‒12 m/s). The temperature during the day varied between +2 and +11°C, with an average of +8°C. Information about the level of solar radiation, ambient temperature, and wind speed comes from the internet weather service [32] and additionally from the NASA MERRA-2 model [33].
A detailed temperature measurement of the panel and radiator was performed using the Seek Thermal ShotPRO thermal imaging device. Figures 8 and 9 show a photo of the solar panel taken with a thermal imaging camera.


The reduction of the mean temperature of the solar panel was calculated according to model (1) for the uncovered ribbed radiator (2).
Figure 10 shows theoretical calculations of the temperature of the panel without cooling and with a passive cooling system during the day and experimental measurements of the temperature of the solar panel using the above thermal imaging camera. Analysis of this chart shows a good match between the theoretical calculations and the experimental data.

The average temperature of the module during the day without a cooling system is 12.3°C, while with the cooling system the theoretical temperature is 11.0°C and the experimental temperature is 10.2°C.
4. Summary and conclusions
The use of Solidworks Flow Simulation to CFD modeling of solar panels allows one to evaluate the thermal state of photovoltaic panels and the effectiveness of a passive cooling system of any material, size and shape.
The coefficients σ, τ,λ, m, n in expression (1) determining the temperature drop using a radiator are depending on its design, the angle of inclination of the solar panel, the direction of the wind at the location of the panel, the distance to the limiting planes (other panels) and can be determined on the basis of the performed simulation.
Application of the proposed method for estimation of the thermal state of solar panels with a passive cooling system enables estimation of the energy production of solar panels installed in any location at a defined time.
The research was financed by a research grant 0211/SBAD/0223.
REFERENCES
[1] Rynek Fotowoltaiki w Polsce 2022 (Photovoltaic market in Poland 2022), https://ieo.pl/pl/raport-pv 2022, access: 15.03.2022.
[2] SolarPower Europe, Global Market Outlook for Solar Power 2021‒2025, https://www.solarpowereurope.org/global-marketoutlook-2021-2025/, access: 20.7.2021.
[3] Photovoltaic Energy Factsheet, Center for Sustainable Systems, University of Michigan. 2022, Pub. No. CSS07-08.
[4] Siecker J., A review of solar photovoltaic systems cooling technologies, Renew. Sustain. Energy Rev. 79 (2017) 192-203.
[5] Sayigh A., Comprehensive Renewable Energy, Photovoltaic Solar Energy, Volume One, Elsevier Ltd, 2012, P.746.
[6] Sato D., Yamada N., Review of photovoltaic module cooling methods and performance evaluation of the radiative cooling method, Renew. Sustain. Energy Rev. 104 (January) (2019), 151-166.
[7] Асанов М.М., Бекиров Э.А., Воскресенская С.Н., Снижение влияния нагрева поверхности фотоэлемента на эффективность его работы (Reducing the effect of solar cell surface heating on its efficiency), Строительство итехногенная безопасность, No 51. (2014), pp. 92-96.
[8] Parkunam N., Pandiyan L., Navaneethakrishnan G., Arul S., Vijayan V., Experimental analysis on passive cooling of flat photovoltaic panel with heat sink and wick structure, Energy Sources, Part A Recovery, Util. Environ. Eff. (2019), https://doi.org/10.1080/15567036.2019.1588429.
[9] Firoozzadeh M., Shiravi A.H., Shafiee M., An experimental study on cooling the photovoltaic modules by fins to improve power generation: economic assessment, Iranian (iranica), Journal of Energy and Environment 10(2) (2019) 80-84, https://doi.org/10.5829/ijee.2019.10.02.02.
[10] El Mays A., et al., Improving photovoltaic panel using finned plate of aluminum, Energy Procedia, 119 (2017) 812-817.
[11] Chen H., Chen X., Li S., Ding H., Comparative study on the performance improvement of photovoltaic panel with passive cooling under natural ventilation, Int. J. Smart Grid Clean Energy, (2014), https://doi.org/10.12720/sgce.3.4.374-379.
[12] Arifin Z., Danardono Dwi Prija Tjahjana D., Hadi S., et. al., Numerical and experimental investigation of air cooling for photovoltaic panels using aluminum heat sinks, Int. J. Photoenergy (2020), 1574274, https://doi.org/10.1155/2020/1574274.
[13] Gotmare J.A., Borkar D.S., Hatwar P.R., Experimental investigation of PV panel with fin cooling under natural convection, Int. J. Adv. Technol. Eng. Sci., 03 (02) (2015) (February).
[14] Bayrak F., Oztop H.F., Selimefendigil F., Effects of different fin parameters on temperature and efficiency for cooling of photovoltaic panels under natural convection, Sol. Energy, 188 (2019) 484-494.
[15] Hernandez-Perez J.G., Carrillo J.G., et. al., Thermal performance of a discontinuous finned heatsink profile for PV passive cooling, Applied Thermal Engineering, 184 (2021) 116238, https://doi.org/10.1016/j.applthermaleng.2020.116238.
[16] Popovic C.G., Hudis teanu S.V., Mateescu T.D., Chereches N.- C., Efficiency Improvement of Photovoltaic Panels by Using Air Cooled Heat Sinks, Energy Procedia, 85 (2016) 425-432.
[17]Jobair H., Improving of photovoltaic cell performance by cooling using two different types of fins, International Journal of Computer Applications (0975–8887), Volume 157 – No 5, (2017) (January)
[18] Freegah B., Hussain A.A., Falih A.H., Towsyfyan H., CFD analysis of heat transfer enhancement in plate-fin heat sinks with fillet profile: Investigation of new designs, Therm. Sci. Eng.Prog., 17 (December) (2019), p. 2020, DOI: 10.1016/j.tsep.2019.100458.
[19] Tijani A.S., Jaffri N.B., Thermal analysis of perforated pin-fins heat sink under forced convection condition, Procedia Manuf., 24 (2018), pp. 290-298, DOI: 10.1016/j.promfg.2018.06.025.
[20] Pal V., Modeling and thermal analysis of heat sink with scales on fins cooled by natural convection, Int. J. of Research in Eng. and Technology, 03(06), 2014, pp. 359-362, DOI: 10.15623/ijret.2014.0306067.
[21] Parihar S., Randa R., Thermal Analysis of Heat Sink Using Solidworks, J. of Emerging Technologies and Innovative Research (JETIR), 8 (10), 2021, pp. 167-175.
[22] Jakhrani A.Q., Othman A.K., Rigit A.R.H., Samo S.R., Comparison of Solar Photovoltaic Module Temperature, ModelsWorld Applied Sciences Journal, 14:1-8.
[23] Website of Sandia National Laboratory (SNL), To Improve PV Performance ModelingCollaborative (PVPMC1), https://pvpmc. sandia.gov/modeling-steps/2-dc-moduleiv/module-temperature/sandia-module-temperature-model/, access: 11.08.2016.
[24] Faiman D., Assessing the outdoor operating temperature of photovoltaic modules, Prog. Photovolt. Res., Appl. 16 (2008) 307-315, http://dx.doi.org/10.1002/pip.
[25] Obuchow S., Plotnikow I., Model symulacyjny trybów pracy autonomicznej stacji fotowoltaicznej z uwzględnieniem rzeczywistych warunków pracy, Wiadomości z Tomskiego Uniwersytetu Politechnicznego. Inżynieria geodezyjna, 2017. T. 328. No 6., 38-51.
[26] Muzathik A.M., Photovoltaic Modules Operating Temperature Estimation Using a Simple Correlation, International Journal of Energy Engineering, Aug. 2014, vol. 4, Iss. 4, 151-158.
[27] Akhsassi. M., El Fathi A., Erraissi N., et. al., Experimental investigation and modeling of the thermal behavior of a solar PV module, Sol. Energy Mater. Sol. Cells, 2018, 180, 271-279.
[28] Skoplaki E., Boudouvis A.G., Palyvos J.A., A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting, Sol. Energ. Mat. Sol. C., 2008, 92:1393-1402.
[29]Yang R., Tiepolo G.,Tonolo E.,Junior J.,Souza M., Photovoltaic Cell Temperature Estimation for a Grid-Connect Photovoltaic Systems in Curitiba, Brazilian Archives of Biology and Technology. Vol.62 no.spe: e19190016, 2019 http://www.scielo.br/babt
[30] Oh J., Pavgi A., Tamizhmani G., Determination of Empirical Coefficients and ΔT for Sandia Thermal Model: Dependence on Backsheet Type, proc. of 7th World Conference on Photovoltaic Energy Conversion (WCPEC-7), 2018, pp. 442-446.
[31] Holovko O., Badanie efektywności energetycznej systemu pasywnego chłodzenia paneli słonecznych w klimatycznych warunkach regionu Kujawsko-Pomorskiego (Research on the energy efficiency of a passive cooling system for solar panels in the climatic conditions of the Kuyavian-Pomeranian region). master thesis, Wyższa Szkoła Gospodarki w Bydgoszczy, 2022.
[32] MSN Weather, https://www.msn.com/pl-pl/pogoda/prognoza/inPoznan, access: 17.01.2022.
[33] ArcGIS World Geocoding Service, Prediction Of Worldwide Energy Resource, POWER | Data Access Viewer, https://power.larc.nasa.gov/data-access-viewer/, access: 17.03.2022.
Authors: M.Sc. Oleh Holovko, Poznan University of Technology, Institute of Automatic Control and Robotics, 3a Piotrowo Street, 61- 138 Poznań, E-mail: oleh.holovko@put.poznan.pl; PhD Eng. Adam Konieczka, Poznan University of Technology, Institute of Automatic Control and Robotics, 3a Piotrowo Street, 61-138 Poznań, E-mail: adam.konieczka@put.poznan.pl; prof. dr hab. Eng. Adam Dąbrowski, Poznan University of Technology, Institute of Automatic Control and Robotics, 3a Piotrowo Street, 61-138 Poznań, E-mail: adam.dabrowski@put.poznan.pl.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 99 NR 10/2023. doi:10.15199/48.2023.10.54