Published by Ahmed M. Agwa1,2, Shaaban M. Shaaban1,3,
Northern Border University (1), Al-Azhar University (2), Menoufia University (3), Egypt
Abstract. Each power plant (PP) is solo entity whose construction site is determined by different criteria in accordance with some physical rules. Latterly, great importance is provided to siting PP in inexact surroundings. Multiple-criteria decision-making for the proper location of the PP construction is relevant. The objective of this research is to create a model for decision-makers to rank available sites for installing hydropower plant (HPP) in accordance with multiple-criteria attributes e.g. accessibility to electrical grid, power potential, economical respects, environmental influence, topography, and natural hazards. In this research, a novel application of a hybrid approach that employs rough set theory (RST) and combinative distance-based assessment (CODAS) method is proposed to prioritize available locations for installing HPP. Firstly, the strength of RST is adopted to get minimal attributes reduction set. Secondly, the relative weights of minimal attributes are determined using RST. Finally, CODAS technique is utilized to calculate the rank of alternatives. The comparison between the proposed method-based results and the results without attributes reduct, proves that the proposed method saves the time and energy.
Streszczenie. Zaproponowano nowatorskie zastosowanie podejścia hybrydowego, które wykorzystuje teorię zbiorów przybliżonych (RST) i metodę oceny kombinowanej opartej na odległości (CODAS) w celu ustalenia priorytetów dostępnych lokalizacji do zainstalowania elektrowni wodnej (HPP) zgodnie z atrybutami wielokryterialnymi, np. dostępność do sieci elektrycznej, potencjał energetyczny, aspekty ekonomiczne, wpływ środowiska, topografia i zagrożenia naturalne. (Planowanie usytuowania elektrowni wodnej metodą wstępną i kombinowanąocena na podstawie odległości).
Keywords: Hydropower plant, site selection, multiple-criteria decision-making, rough set, combinative distance-based assessment
Słowa kluczowe: Elektrownia wodna, wybór miejsca, podejmowanie decyzji według wielu kryteriów, zgrubny zestaw, kombinowana ocena oparta na odległości
Introduction
Global warming has caused by the increase in industrial activities and unrestrained usage of fossil fuels. Consequently, the climate of several places is unforeseeable nowadays and has turned into unusual. Therefore, the hydropower importance arises as one from the best sources of renewable energy which is distinguished as environmentally friendly, safe, sustainable, and economical [1, 2].
Selecting the best site for installing hydropower plant (HPP) is a tremendously complex procedure as various and contradictory criteria need to be studied in detail. In general, the dependence of the feasibility of installing a power plant (PP) on location, results in a multiple-criteria decision making (MCDM) problem. During the procedure of siting PP, there are quantifiable and epistemic uncertain criteria. The uncertain criteria associated can be modeled correctly by means of an algorithm which imitates natural intelligence.
Throughout installing industrial locations like PPs, numerous hurtful elements that are dangerous to environment and living organisms will augment due to reducing the area of large forests in erection stage and pollutants. Moreover, hurtful gases may be emitted owing to the combustion of fuel in the thermal PPs. Our already highly polluted environment will deteriorate by irresponsibly and improperly siting the PP construction. Consequently, environment influence evaluation (EIE) is habitually executed after determining possible site for installing an industrial plant. EIE procedures act as a strict requirement in siting for long time and have presently attracted researchers’ interests.
Criteria e.g. accessibility to electrical grid and economical respects also act significant roles in siting PPs. During siting HPP, water flow rate and watery head are important criteria since the output power of HPP is directly proportional to them.
Numerous researchers have aimed to prioritize available locations for installing PPs by means of several approaches. Particularly, geographical information system (GIS) [3-9], ordered weighted averaging accompanied by linear weighted averaging [10], artificial neural networks learned by genetic algorithm [11], neuro-fuzzy structure [12], technicality of ordering preference using similarities to ideal solution (TOPSIS) accompanied by vlše kriterijumska optimizacija kompromisno rešenje (VIKOR) (which can be translated from Bosnian to English, better criterion optimization compromise solution) [13], and analytic hierarchy process (AHP) [14].
Other approaches like fuzzy logic (FL) [15,16], FL accompanied by TOPSIS [17-19], FL accompanied by both of AHP and TOPSIS [20, 21], expert system [22], and linear programming [23], were applied to rank available sites for installing PPs.
In addition to the above approaches there are others have been utilized to grade available locations for installing PPs such as graph theory accompanied by matrix method [24], multi-attribute choquet integral [25], hierarchical decision model [26], resources spatial and temporal conjunction [27], and rough set theory (RST) accompanied by multi-objective programming [28].
With reference to the above brief survey, it is still a room for ranking available sites for installing HPP. In this regard, the research will address RST and combinative distance based assessment (CODAS), which was designed in 2016 [29], in order to grade available locations for installing HPP since published results of RST and CODAS are hopeful and verify their preference over other methods.
RST
RST can be utilized to draw out knowledge from a scope in a brief manner while preserving the content of the information [30]. In RST, distinguishing two objects acts a critical role for choosing a feature [31].
Knowledge Systems
Assume an information system (OB, ATT, VAL, f), where OB – a non-empty group of objects and ATT – a nonempty group of limited attributes, VAL – a group of values of attributes, f – a mapping which from OB to VAL, and fa(x) means the value of attribute a of object x.
Indistinguishability Relation
In RST, an equivalence relation RA is the base of sorting procedure and it can be stated w.r.t. to A (where A ⊆ ATT) as stated in (1).
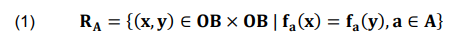
If (x, y) ∈ RA, then it is said that x and y are indistinguishable using attributes from A. Equivalence classes created by equivalence relation RA are called as categorization [x]A.
Approximations of Sets
Upper and lower approximations of X ⊆ OB, are stated as below:
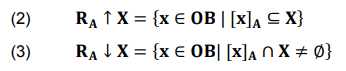
Rough set is the ordered pair (RA ↓ X, RA ↑ X).
Dependency of Attributes
An evaluation of dependency of two attributes sets A, B ⊆ ATT is presented in RST. The evaluation is called a degree of dependence of A on B (γB(A)) and stated in (4).

where card – the set cardinality and POSB(A) – a positive zone of categorization [x]A (or shortly a positive zone of A) for B. The set POSB(A) includes the objects of OB that perhaps be categorized as pertaining to one equivalence class of RA, utilizing attributes from B. The parameter γB(A) determines ratio of the objects that can be correctly categorized. It can be said that A relies on B to degree γB(A). The value of γB(A) ranges from 0 to 1.
Importance of Attributes
The parameter γ is utilized to identify a vital conception for investigations about importance of an attribute as revealed in (6).
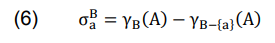
where σBa– the importance of an attribute a, a ∈ B, B ⊆ ATT, which indicates how significant the attribute a is in B, concerning categorization [x]A. Removal of attribute a is tested and its importance is determined by the resultant change in categorization [x]A.
The described importance relies on both set A and B so it is relative value. Thus, an attribute perhaps owns different importance for different categorizations and in different sets (set B in (6)). To identify an absolute importance of an attribute in (7), the entire set of attributes ATT is taken as the sets A and B in the description A = B = ATT.
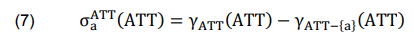
And taking in consideration that γATT (ATT) = 1, then:

Attributes Reduct and Core Attributes
Suppose an attribute a, a ∈ B, B ⊆ ATT, if POSB([x]A) = POSB−{a}([x]A), then a is redundant to B, concerning [x]A, otherwise a is indispensable.
If RB = RATT and POSB([x]A) ≠ POSB−{a}([x]A), then B is named a reduct subset for information system and symbolized as RED(ATT); the intersection of these reduct subsets is called core and symbolized as CORE = ⋂RED(ATT).
Weights of Attributes
When each attribute importance is normalized, each attribute weight (wti) can be obtained as stated in (9).
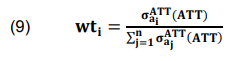
CODAS
CODAS is a modern method utilized efficiently in MCDM. In this technique, the desirability of all obtainable alternates is measured based on two criteria, first of them, the Euclidean spacing (l2 -norm) measurement between every alternate and the worst solution. The second criterion is the corresponding measurement of Taxicab spacing (l-norm) [32]. It’s obvious that the alternate that owns larger spacing from the worst solution is more desired. In this technique, if two alternates are incomparable in accordance with the Euclidean spacing, the Taxicab spacing will be utilized as secondary measurement [33]. Assume that there are m alternates and k criteria. The steps of CODAS for MCDM are as following:
1st Step
The decision-making matrix (X), is constructed as below:
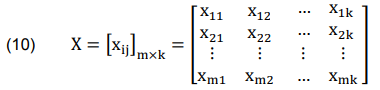
where xij (xij > 0) – the value of performance of alternate i on criterion j (i ∈ {1, 2…, m} and j ∈ {1, 2…, k}).
2nd Step
The matrix of normalized values (nij) of performance, is computed using linear normalization as following:
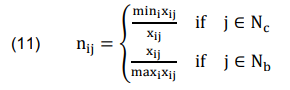
where Nc,Nb – the groups of cost and benefit criteria, consecutively
3rd Step
The matrix of the weighted normalized values (rij) of performance, is computed as follows:
rij = wtjnij
where wtj – the weight of criterion j, which is computed using (9) and subjected to the two following conditions:
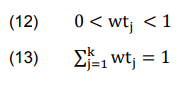
4th Step
The worst solution (ws) is the minimum value of the weighted normalized values of performance as calculated below:
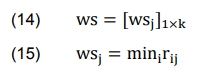
5th Step
The Euclidean spacing (Ei) and Taxicab spacing (Ti) between alternates and the worst solution, are computed as below:
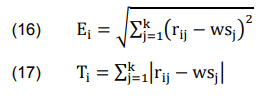
6th Step
The relative assessment matrix (RE) is constructed, as following.
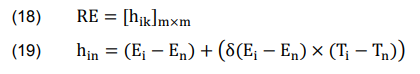
where n ∈ {1, 2…, m} and δ – a threshold function for determining whether two alternates own equal Euclidean distances or not, and is stated as below:
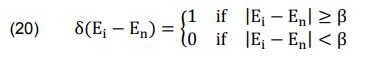
where β – the threshold parameter which the decisionmakers had defined. The value of β is between 0.01 and 0.05.
Two alternates will be compared using the Taxicab distance as an additional value if the variance between their Euclidean distances is less than β. In this paper, β = 0.02 is utilized for the computations.
7th Step
The assessment score for every alternate, is calculated as following:
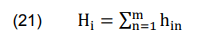
8th Step
The alternates are ranked in descending order in accordance with the assessment scores values.
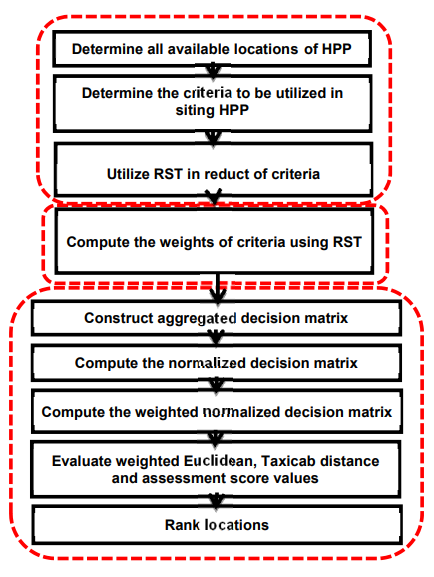
The flowchart in Fig. 1 displays the steps of the suggested approach including RST and CODAS for siting HPP.
Results, Validations, and Discussions
In this section, a case study located in northern Iran is tested to legalize the performance and the effectiveness of the suggested approach in MCDM for sitig HPP.
Knowledge System of Siting HPP
Table 1 includes the required information system for RST about available locations of HPP. Twenty-two available locations (Loc1, Loc2…, Loc22) and twelve conditional attributes (ca1, ca2…, ca12) with their values are displayed in Table 1. Decision attribute (DA) indicates the level of suitability (0 for low appropriateness, 1 for medium appropriateness, 2 for high appropriateness). Interpretations of conditional attributes (ca1, ca2…, ca12) and their values (1, 2, 3) are revealed in Table 2.
Categorization and attributes dependency, which are computed using (1) to (5), are not mentioned to avoid boring lengthy article to the readers but their values are utilized to calculate the reduct and importance of attributes.
Attributes Reduct by RST
The consistency of appropriateness level with twelve conditional attributes is tested during this stage. For extracting reduct using RST, redundant attributes need to be defined and a decision table is required to be created free of inconsistencies. To find the redundant attributes of assessments, removal of attributes one by one is tested, and the categorization is checked each time to insure no inconsistency has arisen. The results reveal that a2, a6, a7, a9, a10, a11, a12 are redundant attributes and a1, a3, a4, a5, a8 are indispensable attributes. That is to say, accessibility to electrical grid, water flow rate, watery head, economical respects, and topography are the core for appropriateness level for siting HPP and the other indices can be omitted because they are unnecessary information for siting HPP. Consequently, Table 3 is gotten by removing the redundant attributes from Table 1.
Determination of Importance and Weights of Attributes by RST
The importance of the core attributes ca1, ca3, ca4, ca5, ca8 is calculated using (8) and the results are 0.091, 0.227, 0.227, 0.136, 0.091 respectively. The attributes weight of ca1, ca3, ca4, ca5, ca8 is calculated by normalization of attribute importance using (9) as revealed in (23) to (27).

Table 1. Information system of siting HPP
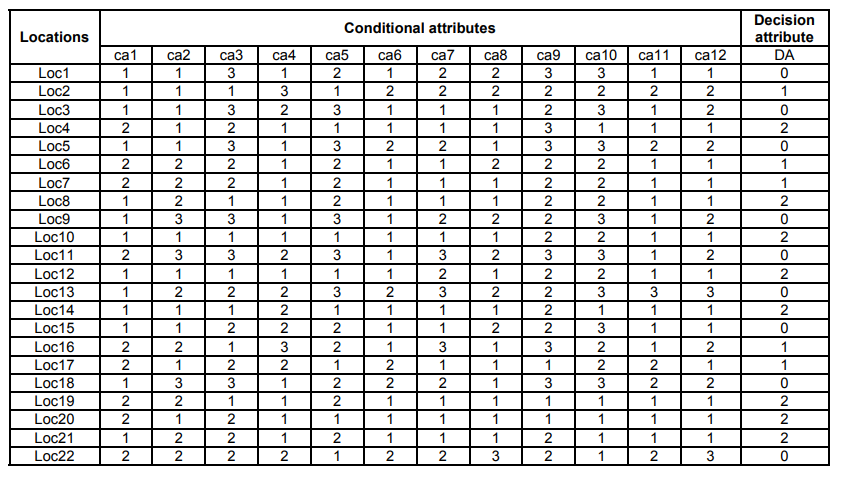
Table 2. Conditional attributes and their values
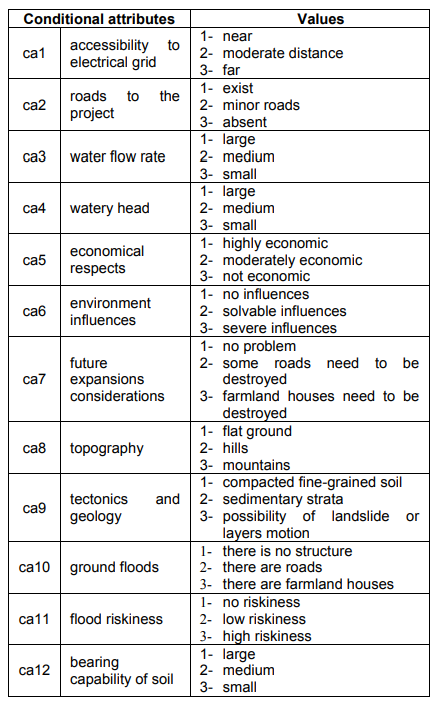
Table 3. Core attributes
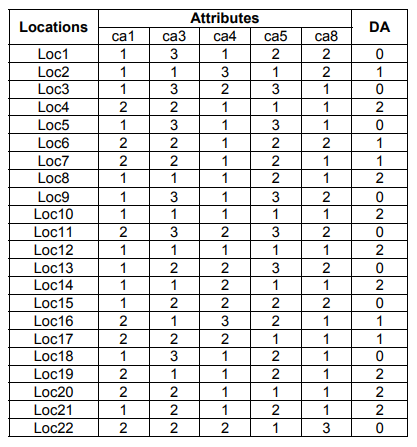
Ranking the Available Locations of HPP by CODAS
After determination of the criteria weights by RST, the rank of HPP sites is obtained using CODAS. In CODAS, firstly decision-making matrix is constructed in Table 4.
In siting HPP problem, ca1, ca3, ca4, ca5, ca8 criteria are cost criteria because they are desired to be minimized. The matrix of normalized values of performance is computed in Table 5 using (11).
The weighted normalized performance values and the worst solution are computed in Table 6 using (12) and (16), consecutively.
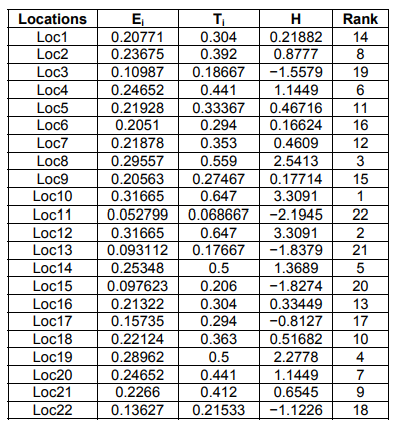
The Euclidean and Taxicab distances between alternatives and the worst solution are computed in Table 7 using (17) and (18), consecutively. The relative assessment matrix is computed using (20). The assessment scores (Η) of alternatives are computed using (22) and the locations are ranked in descending order in accordance with H values as revealed in Table 7.
Table 4. Decision-making matrix
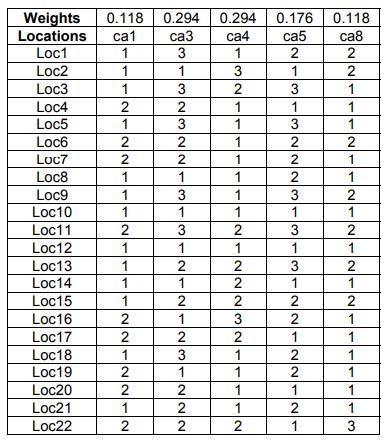
Table 5. The matrix of normalized values of performance
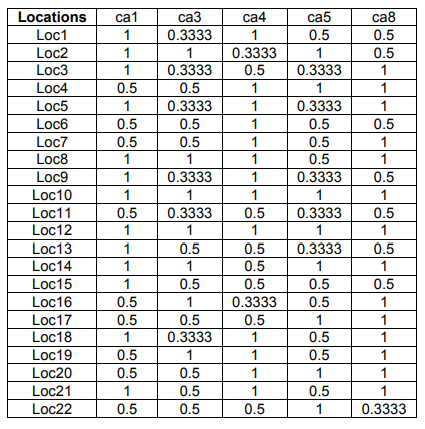
Table 6. The matrix of the weighted normalized values of performance and the worst solution
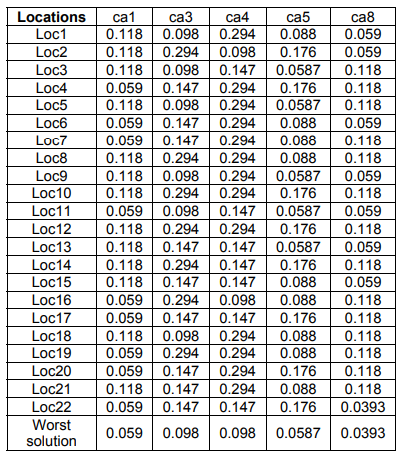
Table 7. Rank of alternatives
Results without Attributes Reduct
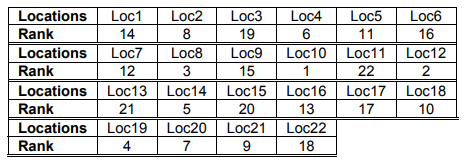
In the previous subsection, the alternatives order for siting HPP is gotten by CODAS after using RST with attributes reduct. In this section, the same case study is tested without attributes reduct to prove usefulness and effectiveness of the proposed method in MCDM for siting HPP. All the criteria in Table 1 are going to be utilized to make a decision. Table 8 displays the criteria weights when utilizing all criteria. Therefore, the rank of all locations is revealed in Table 9.
Obviously, the same rank is obtained and the most desirable choice in two different situations is identical. Consequently, the proposed approach is proved to be useful and effective tool in siting HPP. Furthermore, the proposed approach saves much time and energy due to attributes reduct by RST and avoids human perceptions and judgments using information entropy weight which is dependent on the real data.
Table 8. The attributes weights without attributes reduct

Table 9. Rank of alternatives without attributes reduct
Conclusions
Rank of the available locations for installing HPP can be considered as MCDM problem. Hybrid approach of RST and CODAS has been presented for this purpose. RST is utilized for attributes reduct and attributes weights calculation. CODAS is utilized for locations rank determination. The obtainable sites for installing HPP are ranked by the proposed approach for a case study placed in northern Iran. The same case study is tested without attributes reduct. Sameness of the gotten results in two states verifies that the proposed approach is characterized by good performance, efficacy and saving in the required time and energy. Hence, the proposed approach can be recommended as MCDM tool for siting PPs other than HPP.
REFERENCES
[1] Sowinski J., Green Paper – challenges to RES development in Poland, Przegląd Elektrotechniczny, 90 (2014), No. 4, 145-148.
[2] Paska J., Pawlak K., Ronkiewicz P., Terlikowski P., Wojciechowski J., Polish hydropower resources and example of their utilization, Przegląd Elektrotechniczny, 96 (2020), No. 1, 1-5.
[3] Zaidi A.Z., Khan M., Identifying high potential locations for runof-the-river hydroelectric power plants using GIS and digital elevation models, Renewable and Sustainable Energy Reviews, 89 (2018), 106-116.
[4] Moiz A., Kawasaki A., Koike T., Shrestha M., A systematic decision support tool for robust hydropower site selection in poorly gauged basins, Applied Energy, 224 (2018), 309-321.
[5] Romanelli J.P., Silva L.G.M., Horta A., Picoli R.A., Site selection for hydropower development: a GIS-based framework to improve planning in Brazil, Journal of Environmental Engineering, 144 (2018), No. 7, 1-10.
[6] Sanchez-Lozano J.M., García-Cascales M.S., Lamata M.T., Identification and selection of potential sites for onshore wind farms development in Region of Murcia, Spain, Energy, 73 (2014), 311-324.
[7] Larentis D.G., Collischonn W., Olivera F., Tucci C.E.M., Gisbased procedures for hydropower potential spotting, Energy, 35 (2010), 4237-4243.
[8] Lakshmi S.V., Sarvani G.R., Selection of suitable sites for small hydropower plants using Geo-Spatial technology, International Journal of Pure and Applied Mathematics, 119 (2018), No. 17, 217-240.
[9] Kaliraj S., Malar V.K., Geospatial analysis to assess the potential site for coal based thermal power station in Gujarat, India, Advances in Applied Science Research, 3 (2012), No. 3, 1554-1562.
[10] Temel P., Evaluation of potential run-of river hydropower plant sites using multi-criteria decision making in terms of environmental and social aspects, MSc thesis, Middle East Technical University, (2015).
[11] Shimray B.A., Singh K.M., Khelchandra T., Mehta R.K., Ranking of sites for installation of hydropower plant using MLP neural network trained with GA: a MADM approach, Computational Intelligence and Neuroscience, 2017 (2017), 1-8.
[12] Shimray B.A., Singh K.M., Khelchandra T., Mehta R.K., A new MLP–GA–Fuzzy decision support system for hydro power plant site selection, Arabian Journal for Science and Engineering, 43 (2018), 6823-6835.
[13] Adhikary P., Roy P.K., Mazumdar A., Selection of small hydropower project site: a multi-criteria optimization technique approach, ARPN Journal of Engineering and Applied Sciences, 10 (2015), No. 8, 3280-3285.
[14] Silva H., Blengini A., Mota L., Pezzuto C., Lavorato M., Carvalho M., Multi-criteria analysis of Brazilian wind farms, International Journal of Renewable Energy Research, 10 (2020), No. 2, 1042-1053.
[15] Erol İ., Sencer S., Özmen A., Searcy C., Fuzzy MCDM framework for locating a nuclear power plant in Turkey, Energy Policy. 67 (2014), 186-197.
[16] Deveci M., Cali U., Kucuksari S., Erdogan N., Interval type-2 fuzzy sets based multi-criteria decision-making model for offshore wind farm development in Ireland, Energy, 198 (2020), 117317.
[17] Wang C.N., Su C.C., Nguyen V.T., Nuclear power plant location selection in Vietnam under fuzzy environment conditions, Symmetry, 10 (2018), 548.
[18] Kurt Ü., The fuzzy TOPSIS and generalized Choquet fuzzy integral algorithm for nuclear power plant site selection – a case study from Turkey, Journal of Nuclear Science and Technology, 51 (2014), No. 10, 1241-1255.
[19] Erdebilli B., Yildizbasi A., Arikan Ü.Z.B., Using intuitionistic fuzzy TOPSIS in site selection of wind power plants in Turkey, Advances in Fuzzy Systems, 2018 (2018), 6703798.
[20] Locatelli G., Mancini M., A framework for the selection of the right nuclear power plant, International Journal of Production Research, 50 (2012), no. 17, 4753-4766.
[21] Erdogan M., Kaya I., A combined fuzzy approach to determine the best region for a nuclear power plant in Turkey, Applied Soft Computing, 39 (2016), 84-93.
[22] Sambasivarao K., Raj D.K., Dua D., An expert system for site selection of thermal power plants, Journal of Basic and Applied Engineering Research, 1 (2014), No. 8, 36-40.
[23] Cho S., Kim J., Multi-site and multi-period optimization model for strategic planning of a renewable hydrogen energy network from biomass waste and energy crops, Energy, 185 (2019), 527-540.
[24] Dev N., Attri R., Site selection for a power plant using graph theory and matrix method, Twelfth AIMS International Conference on Management, (2015), 1328-1335.
[25] Cebi S., Kahraman C., Using multi attribute Choquet integral in site selection of wind energy plants: the case of Turkey, Journal of Multiple-Valued Logic and Soft Computing, 20 (2013), 423-443.
[26] Lingga M.M., Developing a hierarchical decision model to evaluate nuclear power plant alternative siting technologies, PhD thesis, Portland State University, (2016).
[27] Jurasz J., Mikulik J., Site selection for wind and solar parks based on resources temporal and spatial complementarity – mathematical modelling approach, Przegląd Elektrotechniczny, 93 (2017), No. 7, 86-91.
[28] Feng R., Optimal site selection for thermal power plant based on rough sets and multi-objective programming, International Conference on E-Product E-Service and E-Entertainment (ICEEE), (2010), 1-5.
[29] Ghorabaee M.K., A new combinative distance-based assessment (CODAS) method for multi-criteria decisionmaking, Economic Computation and Economic Cybernetics Studies and Research, 50 (2016), No. 3, 25-44.
[30] Yu J., Li Y., Chen M., Zhang B., Xu W., Decision-theoretic rough set in lattice-valued decision information system,” Journal of Intelligent & Fuzzy Systems, 36 (2019), 3289-3301.
[31] Tiwari A.K., Shreevastava S., Subbiah K., Som T., An intuitionistic fuzzy-rough set model and its application to feature selection, Journal of Intelligent & Fuzzy Systems, 36 (2019), 4979-4969.
[32] Badi I.A., A. Abdulshahed M., Shetwan A.G., Supplier selection using combinative distance-based assessment (CODAS) method for multi-criteria decision-making, The 1st International Conference on Management, Engineering and Environment (ICMNEE), (2017), 395-407.
[33] Dahooei J.H., Zavadskas E.K., Vanaki A.S., Firoozfar H.R., Keshavarz-Ghorabaee M., An evaluation model of business intelligence for enterprise systems with new extension of CODAS (CODAS-IVIF), Ekonomie a Management, 21 (2018), No. 3, 171-187.
Authors: Ahmed Mahmoud Agwa, Electrical Engineering Department, Faculty of Engineering, Northern Border University, Arar 1321, Saudi Arabia & Electrical Engineering Department, Faculty of Engineering, Al-Azhar University, Cairo 11651, Egypt, Email: ah1582009@yahoo.com; Shaaban Mohamed Shaaban, Electrical Engineering Department, Faculty of Engineering, Northern Border University, Arar 1321, Saudi Arabia & Department of Engineering Basic Science, Faculty of Engineerin, Menoufia University, Shebin El-Kom 32511, Egypt, E-mail: shabaan27@gmail.com
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 97 NR 3/2021. doi:10.15199/48.2021.03.03