Published by Wojciech NITA1, Sylwester FILIPIAK2, PGE Dystrybucja S.A. Oddział Skarżysko-Kamienna (1), Politechnika Świętokrzyska (2)
Abstract. This article elaborates on and supplements the research presented in earlier works [19,20,21] on planning for upgrading field MV power grids. While that study developed models for optimizing failure rates (SAIFI, SAIDI, MAIFI) for large areas of the grid, this paper focuses on applying optimization algorithms to more detailed planning for upgrading individual MV lines from the transformer station selected for analysis..
Streszczenie. Niniejszy artykuł zawiera rozwinięcie i uzupełnienie badań przedstawionych we wcześniejszych pracach [19,20,21] dotyczących planowania modernizacji terenowych sieci elektroenergetycznych SN. W tamtych badaniach opracowano modele dla optymalizacji wskaźników awaryjności (SAIFI, SAIDI, MAIFI) dla dużych obszarów sieci, natomiast w niniejszym artykule skupiono się na zastosowaniu algorytmów optymalizacyjnych do bardziej szczegółowego planowania modernizacji poszczególnych linii SN z wybranego do analizy GPZ-tu. (Optymalizacja modernizacji terenowych linii elektroenergetycznych SN z zastosowaniem algorytmów ewolucyjnych).
Słowa kluczowe: sieci elektroenergetyczne, optymalizacja, metody ewolucyjne
Keywords: power grids, optimization, evolutionary methods
Introduction
An important issue of the operation of field medium-voltage (MV) distribution power grids is the successive modernization of grid systems to reduce failure rates and improve the efficiency of grid infrastructure [3, 4]. Since power grid systems consist of a very large number of components and use specialized technologies applied to power lines, the problem of planning distribution grid modernization projects is complex.
This article elaborates and complements the research presented in papers [21,22,23] on planning for upgrading field MV power grids. An extension of the optimization models described in the paper [21] is to include criteria for optimizing power distributions and a criterion for optimizing voltage conditions in the analyzed grid, taking into account local conditions including existing or planned to be connected sources of distributed generation (GR).
Earlier works [21,22,23] analyzed large portions of the MV field power distribution grid (the results in the aforementioned works included the analysis of the grid area fed from several transformer stations), in those studies models were developed for optimizing the failure rates (SAIFI, SAIDI, MAIFI) for large areas of the grid, while this article focuses on the application of optimization algorithms for more detailed planning of upgrades of a selected MV line sequentially from the transformer station selected for analysis.
The contribution of new original components to this article involves:
• inclusion in the optimization model of additional criteria for: optimization of power distributions and minimization of voltage deviations at grid nodes,
• implementation of calculations for planning MV line upgrades taking into account distributed generation sources connected or planned to be connected to the line,
• inclusion of structural reliability in computational models and the adaptation of these models to calculations using various reliability indexes,
• development of modifications to the applied evolutionary algorithms (in terms of how solutions are encoded and in terms of recombination operators) for the implementation of calculations for individual MV lines,
• implementation of analysis and determination of the Pareto front for the task of optimizing the planning of MV field line modernization projects.
In Polish and English-language literature on the topic there are published works on the operation of MV distribution grids [2, 30], most often these publications deal with the problems of reconfiguration of distribution grids, among others [16, 17], and the development and expansion of power distribution grids, among others [24, 25, 26], while there are fewer works on the problems of modernization, reconstruction of field MV distribution grids. The need to modernize the country’s field MV power grids is due to various reasons, which include the failure rate of grid equipment resulting from aging processes, as well as the increase in the load on these grids.
Measures that improve the reliability of electric distribution grids can include [14, 20, 21, 31, 32]:
• the use of ICT systems to monitor and reconfigure grids,
• the use of modern switching devices (e.g., reclosers),
• replacement of MV lines having bare conductors with shielded conductors or cable lines,
• increasing the share of MV works performed as works on live wires,
• modernization of transformer stations (reconstruction to the H-5 layout).
Replacing MV overhead lines with strings of MV cable lines is one method of improving grid reliability. Insulated overhead lines are an alternative to cabled MV lines. Another method of improving the reliability of distribution grids is to install modern switching and protection equipment in the grids [31].
The problem of planning the modernization of field MV lines considered in the article requires the use of a nonlinear optimization model, which includes continuous and discrete decision variables. Based on the research conducted (which analyzed the use of various optimization algorithms), it was concluded that in order to solve such a problem, the appropriate methodology would be the use of evolutionary algorithms. These algorithms do not require knowledge of the form of the derivative of the objective function and are robust to discontinuities in the function and to local minima [1, 28, 29]. In the implemented calculations whose results are included in the article, the aggregation approach of criterion functions was taken into account and Pareto sets of optimal solutions were sought.
Calculation methodology used
In order to solve the problem of planning the modernization of field MV lines and optimizing the financial outlay for such projects, various optimization algorithms were analyzed with a focus on population-based heuristic algorithms (including genetic algorithms, particle swarm algorithms [2, 7]). The result of this research was the selection of evolutionary algorithms as particularly predisposed to solve the problem analyzed in the article.
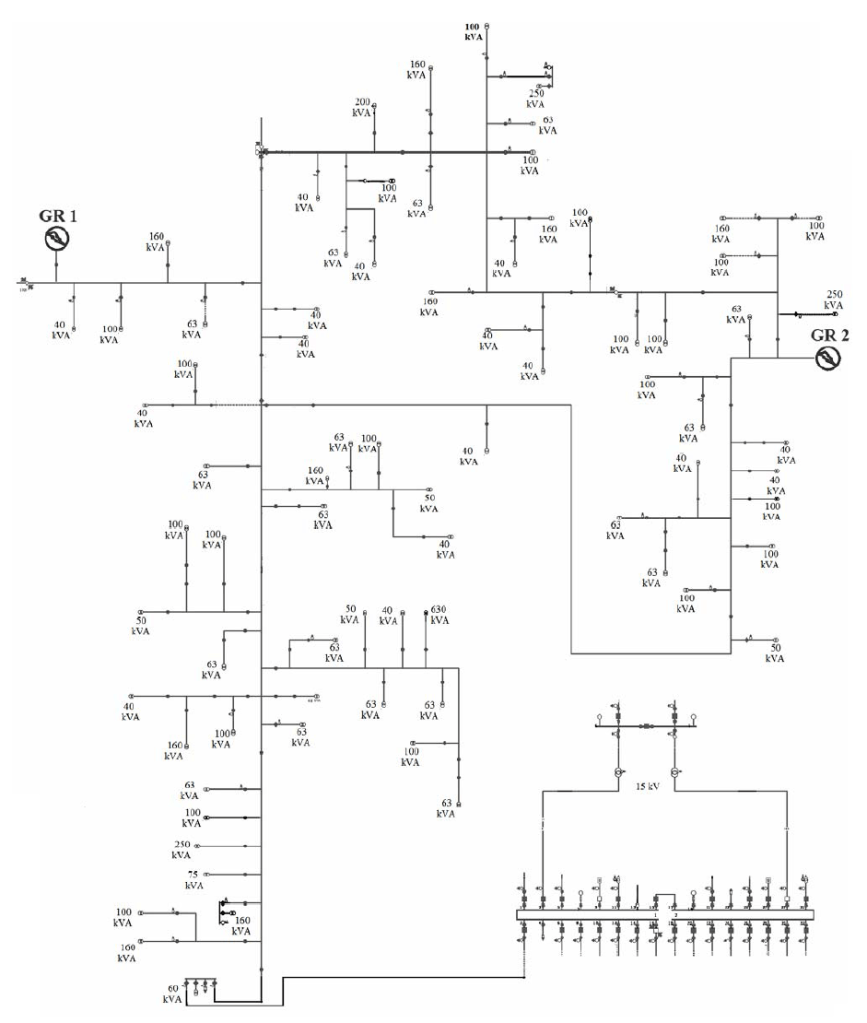
The MV line string fed from the second field of the transformer station of the analyzed grid was selected for the computational analysis, as shown in figure 1. Calculations for other MV lines fed from a given transformer station can be carried out in a similar way. The following criteria were analyzed in the proposed optimization model:
• minimization of grid failure rates (including SAIFI, SAIDI, average failure severity and failure durations),
• optimization of power distributions,
• minimization of voltage deviations at MV grid nodes,
• minimizing technical losses in the distribution grid,
• minimizing expenditures on upgrading the distribution grid under study,
For the optimization model used, limiting conditions relating to the maintenance of correct voltage levels and the maintenance of correct grid load conditions were taken into account. The values of the quantities determining the failure rate of cable lines were adopted on the basis of the studies described in papers [3, 5, 6].
Table 1. Examples of selected actual section data at the ends of MV line branches (data excerpt)
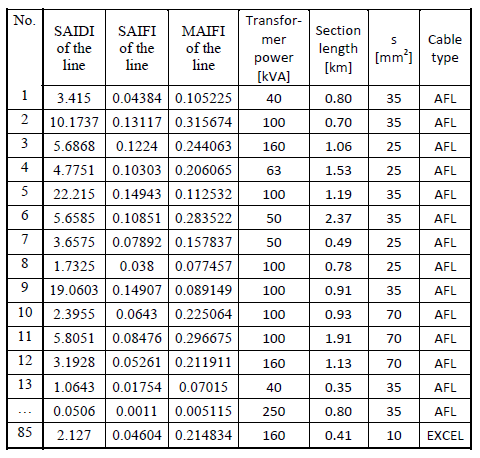
In the first stage of the analyses, analyses using objective functions integrating the adopted optimization criteria were realized. In the second stage, calculations were also carried out to find sets of Pareto-optimal solutions. For this purpose, evolutionary algorithms adapted to multi-criteria calculations were used. The Matlab program and the “MatPower” package [24, 27] were used to perform the calculations. The purpose of the coding method adopted is to identify solutions for multivariate planning of grid upgrades, taking into account the use of distributed generation plant generation capacity.
The decision variables included in the optimization model determine the implementation (or lack thereof) of the upgrade of a specific element of the MV line under analysis. Encoding with a vector of real numbers was used.
In addition, the values of the decision variables also determine the choice of upgrade variant (if more than one variant is considered for a given device). The analyzed variants of section upgrades take into account the fulfillment of technical conditions regarding load capacity, throughput, voltage conditions, short circuit parameters.
The following optimized vector objective function was determined:

f1(x) – refers to the minimization of the SAIFI index (for the analyzed grid), which is a measure of the number of outages per customer (per year), and does not include outages shorter than 3 minutes:
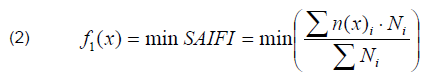
whereas: ni – number of unscheduled outages at customers at a given location, Ni – number of customers at a given location,
f2(x) – refers to minimization of the SAIDI index, determines the total duration of power outages in minutes that a customer in a given area of the distribution grid can expect (during the year):
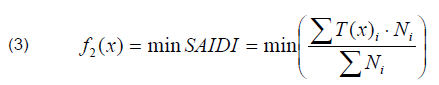
whereas: Ti – annual outage time of customers at a given location, Ni – number of customers at a given location,
f3(x) – determines the minimization of power losses in the analyzed MV grid:

whereas: Rmi – resistance of the i-th section of the line after the upgrade,
f4(x) – the criterion function relates to the minimization of voltage deviations at the nodes of the analyzed field MV grid,

whereas: Ui – voltage at the i-th node, Uo – expected voltage, UN – rated voltage, n – number of nodes,
f5(x) – the criterion function for the criterion under consideration can be represented as the summation of cost functions for individual generation nodes:

where: Q – vector of values of voltage shift angles, Vm – vector of values of nodal voltages, Pg, Qg – vectors of values of generated active and reactive power,
In the developed computational model, the criterion of optimization of power distributions in the grid was taken into account (the description used in the Matpower package was used). Among other things, calculations of optimal power distributions can be carried out using the “runopf” function of the Matpower package, which performs calculations based on Lagrange’s theorem and Kuhn-Tucker conditions.
These conditions are equivalent to the conditions for the existence of the saddle point of the Lagrange function, built on the function f(x) under the limitations gi(x).
The considered optimization task in its general form is described by the formulas [24, 27]:

The limiting conditions are a set of power balance equations described by formulas [24]:
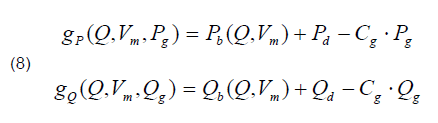
where: Cg – connection matrix which can be defined so that its element (i, j) has a value of 1 if generator j is on bus i and 0 otherwise.
To write the aggregate form of the objective function, the distance function minimization methodology was adopted. The distance function method combines several criterion functions into a single aggregate based on a vector of (arbitrarily determined) ideal values. In this case, the optimal solution is the one that minimizes the distances between F(x) and the y vector.
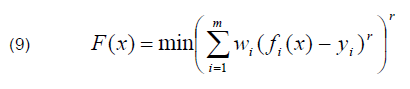
whereas: r = 2 (most commonly used), the following set of weights was used for the optimization calculations for the criterion of reliability maximization and expenditure minimization: (w1=0.8, w2=0.2), (w1=0.7, w2=0.3) … (w1=0.2, w2=0.8). For subsequent calculations, the change of weight values for individual criteria is applied with a step of 0.1 or 0.05 (where the sum of all weights equals 1).
Various sets of criteria were analyzed in the completed computational analyses. In the results presented in the article (due to the volume of the article, selected results are included), instead of the criterion of optimizing power flow, the criterion of minimizing voltage deviations and the criterion of minimizing technical losses in the analyzed MV grid were taken into account.
The operators used in these algorithms changed the values of the decision variables within the limits set by the lower and upper bounds. The calculation methodology used makes it possible to determine the set of sections selected for modernization and the extent of modernization of individual MV lines. By decoding the solutions obtained, it is possible to identify options for upgrading individual sections of the grid. The crossover operator used is based on generating a vector of binary numbers and modifying (within assumed narrow limits) the transferred values of decision variables between solutions.
The calculations were carried out for the MV field electrical distribution grid shown in figure 1.
In the coding method adopted, the values of the decision variables were in the range of 0 ÷ 1. At the same time, the range was divided into four divisions, and depending on the value of the variable, the realization or lack of realization of modernization for the grid element associated with the decision variable was determined.
Based on the value of the decision variable, the option of upgrading a given section of the line was also determined (including the length of the route, the line reconstruction technology used).
Results of computational analyses
Computational analyses were carried out using Matlab and, in particular, the Matpower package [23, 26]. For this purpose, a description of the analyzed grid structure (node and branch data) was developed in the form of Matpower package files, which made it possible to carry out flow calculations.
It has been assumed that 30÷40% of the sections of the analyzed MV power line will be modernized, taking into account the modernization of both the end sections and in the so-called core of the line. A computer model of the MV field power lines adopted for analysis was developed. The analyzed section contains 150 nodes and about 250 branches (MV line sections). The description of the structure and parameters of the analyzed MV (15 kV) distribution grid was made according to the principles used in the Matpower package.
The description of the optimization model includes criterion objective functions, constraint conditions, coding procedures, recombination operators. In the completed analyses, grid loads were taken into account, and the generation capabilities of grid-connected distributed generation sources were considered (for local climatic conditions, the generation capabilities of local distributed generation sources were assumed).
In the main computational loop, the so-called “simulated evolution” calculations are carried out, within which the values of the criterion functions are calculated for the variants of modernization of the analyzed MV power line configured by the algorithm.
The evolutionary algorithm used for the computational analyses, implemented by Matlab’s ag function, used available recombination operators that create new solution variants. On the other hand, task-adapted procedures for encoding and decoding solutions were developed.
Initial analyses were realized for the formulated aggregate objective function described by equation (1). The results obtained are presented sequentially in figures 2÷3. These figures illustrate the course and effect of calculations to find solutions describing the range of projects for optimal MV line modernization plans with a new (compared to the optimization model from the works [21,22,23]) set of optimization criteria.

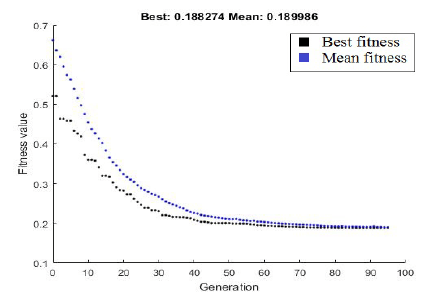
The adopted coding method can be used to record alternative options for upgrading the MV line sections in the analyzed section of the field MV line. Modernization variants may differ in the different ways of routing the line, the technology used, as well as the diagnostic and switching equipment used, and the assumed length over which sections of the modernized MV line are rebuilt.
Figures 4, 5 show the execution of calculations with the assumption that two sources of distributed generation of 1 MW each are connected in the analyzed part of the grid. The calculations performed confirmed the feasibility of using the methodology described in the article to implement optimization calculations taking into account existing distributed sources or distributed sources planned to be installed in the grid.
Subsequent analyses, the outcomes of which are included later in the article, involved calculations considering two distributed sources in the form of photovoltaic farms of 1 MW each, as noted in figure 1.
In the realized analyses, reproducible results were obtained by obtaining solutions with the following consecutive values of the aggregating four criteria of the objective function: 0.198533, 0.198551, 0.198703, 0.198729, 0.198761, 0.198907, 0.199062.
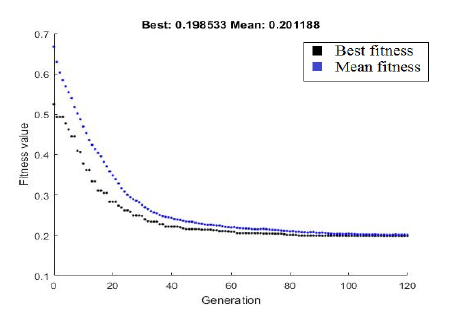
Table 2 shows the best obtained values of the set of criterion functions selected for presentation for the solution found by the evolutionary algorithm that optimized the aggregate objective function. The aggregate functions were written using the method of minimizing the distance function between the values of the criterion functions and the values stored in the vector of ideal values. The found solution is illustrated in the diagram (fig. 11), where the MV line sections selected for upgrading are marked, which provides a graphic interpretation of the results.

Tables 2 and 3 contain a description of the obtained solution in the form of a summary of the best obtained variants for upgrading the field MV line under study. The evolutionary algorithm used processes a population of 150 elemental vectors of real numbers, with a coded variant of the solution. Below are two decoded 150-element vectors in which each element of the vector is assigned a digit, which in turn determines the designated option for upgrading a given section of the MV line under analysis.
These two vectors differ very little (only at two positions) because they represent very similar variants of solutions. In these vectors, zeros indicate no upgrade while the numbers from 1 to 3 specify the upgrade variant for a given section of MV line.
solution variant no. 1 = 1,2,2,0,1,2,0,2,0,1,0,1,0,1,0,2,0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,2,3,3,0,0,2,0,1,0,1,0,0,0,0,0,2,0,1,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1,1,0,1,0,1,0,2,0,0,0,0,0,0,0,0,0,1,0,0,2,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0
solution variant no. 2 = 1,2,2,0,1,2,0,2,0,1,0,1,0,1,0,1,0,2,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,2,3,3,0,0,2,0,1,0,1,0,0,0,0,0,2,0,1,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1,1,0,1,0,1,0,2,0,0,0,0,0,0,0,0,0,1,0,0,2,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0
Table 2. Values of criterion functions for the obtained solutions

Table 3. Values of reliability indexes of MV line sections after modernization

Calculations were also performed to graphically illustrate the obtained Pareto front for the selected two and three criteria for the analyzed problem. Figure 6 illustrates the results of calculations for the two criteria of financial input and reliability of the optimized MV line system. Single points (circles) for the aggregate approach are also plotted in this figure. These points were obtained in subsequent computational experiments in the implementation of which the weighting coefficients for the aggregate objective function for each criterion were empirically selected. This made it possible to find points distributed on the Pareto front for the problem under analysis.

In Figure 6, the SAIFI indexes calculated for the analyzed MV line (after normalization calculations) for the analyzed field MV line are used as a reliability criterion.
This indicator was calculated taking into account the structure of the supply routes of individual consumer nodes with the knowledge of the values of SAIFI indicators for individual sections of the analyzed fragment of the field MV grid. The calculation algorithms have been prepared so that calculations can also be made for all other reliability indexes such as p and q reliability indexes, SAIDI, MAIFI or average failure severity.
Computational analyses using algorithms (NSGA II, NSGA III [7, 8, 10]) that enable multi-criteria optimization calculations with independent treatment of individual criteria have also been realized [28, 29]. The non-dominated vectors of values calculated for the criterion functions form the Pareto front of the solutions. Figures 7 and 8 show the sets of Pareto-optimal solutions determined by each algorithm.
Computational analyses were carried out using normalizing conversions so that the individual values of the criterion functions fell within the range 0 ÷ 1, with arbitrary determination of the maximum and minimum values of the criterion functions in physical units.
The use of calculations normalizing the values of the criterion functions made it possible to unify the graphs presenting the results of the calculations and also allowed to present the concept and methodology of the calculations.
For the computational analyses, it was assumed that the maximum planned expenditures on grid modernization would allow to upgrade about 40% of the total length of the analyzed MV line string, taking into account the length of the line in the line core and all line branches. Fig. 7. Set of Pareto-optimal solutions for the three criteria (obtained with the NSGA II algorithm) Fig. 8. Set of Pareto-optimal solutions for the three criteria (obtained with the NSGA II algorithm with scores obtained for the aggregated approach)
In addition, in normalizing calculations (which facilitated the graphical presentation of the results of the calculations), such minimum and maximum values of financial outlays were selected so that, in particular, solutions close to the full assumed level of expenditures on the modernization of the analyzed MV line were analyzed.
Figure 9 shows the Parteo front obtained with the NSGA II algorithm for the analyzed problem, and indicates with rhombuses the obtained points using the aggregated objective function approach (these solutions are located in the middle part of the Pareto front) after introducing the weighting coefficients into the aggregated objective function, it is also possible to find points located in another part of the Parteo front.
Figures 9 and 10 illustrate the comparison of the sets of Pareto-optimal solutions determined for the analyzed task with the two algorithms (NSGA II and NSGA III [24, 29]). Each of the algorithms used has its own solution finding strategy [10]. The obtained results confirmed the convergence of the obtained solutions. The choice of the final solution in such a case is made by the decision-maker based on additional considerations.
The results for the aggregate objective function were obtained and a set of Pareto-optimal solutions was found for the analyzed problem. After realizing multivariate analyses with different algorithms, solutions were obtained that showed convergence of results.
For example, one of the best solutions obtained in the form of sets of projects that make up the optimal option for upgrading the MV line under study is illustrated in figure 11, the sections selected for upgrading are marked in red.
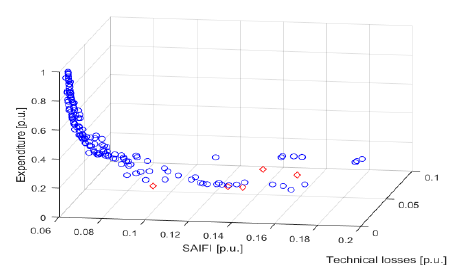


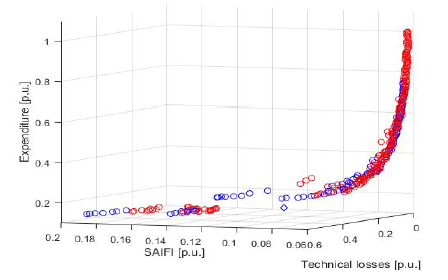
NSGA II and NSGA III algorithms were used to find the Pareto front for the problem under analysis. Among other things, the calculations used the algorithm available in Matlab’s gamultiobj function, which allowed to determine the Pareto front (for selected criteria), which is illustrated in figure 9.
Figure 11 shows in red those sections of the field MV power line that were selected for upgrading as a result of optimization calculations. This type of analysis can be carried out sequentially for all MV power lines coming out of the transformer station selected for analysis.
The solution variant shown in Figure 11 is characterized by the fact that sections of the line located primarily in the core of the line were selected for modernization projects, while sections from the line’s branches were selected to a lesser extent. This can be explained by the fact that the MV line analyzed was characterized by small cross sections, and the sections selected by the algorithm for modernization most urgently required modernization work.

Summary
This article presents a modification and development of computational models previously presented in papers [21, 22, 23]. The computational optimization models from the aforementioned papers were adapted to finding optimal plans for modernizing large parts of the grid (fed from several transformer stations) with a limited number of criteria for an assumed time horizon of several years.
The modifications to the computational models proposed in this article make it possible to optimize reliability and efficiency for selected individual field MV power lines, while taking into account the local operating conditions of the MV lines and the power generated by GR distributed sources connected or planned to be connected.
For the calculations, heuristic methods were used in the form of evolutionary algorithms in the basic version (for the variant of calculations using the aggregate objective function) and the extended version for finding sets of Pareto-optimal solutions. The algorithms presented in the article provide opportunities to determine the scope of modernization activities in the analyzed MV lines fed from individual line fields of the transformer station. The results of the calculations are the optimal variants and scope of upgrading field MV power lines found by the algorithms.
REFERENCES
[1] Abedini M., Moradi M.H.: A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. International Journal of Electrical Power & Energy Systems. Volume 34, Issue 1, January 2012, pp. 66–74.
[2] Acharya N., Mahat P, Mithulananthan N.: An analytical approach for DG allocation in primary distribution network”, International Journal of Electrical Power & Energy Systems, vol. 28, 10, 2016, p.669-678.
[3] Banasik K., Chojnacki A. Ł.: Effects of unreliability of electricity distribution systems for municipal customers in urban and rural areas, Przegląd Elektrotechniczny issue 05/2019, p. 179-183.
[4] Bobric E. C., Cartina G., Grigoras G.: Fuzzy Technique used for Energy Loss Determination in Medium and Low Voltage Networks. Electronics and Electrical Engineering. – Kaunas: Technologija, 2009. – No. 2(90). – P. 95–98.
[5] Chojnacki A.: Assessment of the Risk of Damage to 110 kV Overhead Lines Due to Wind. Energies, 2021, p. 1-14.
[6] Chojnacki A.: Analiza niezawodności eksploatacyjnej elektroenergetycznych sieci Dystrybucyjnych, Monografie studia, rozprawy, Kielce, 2013.
[7] Ciro G., Dugardin F., Yalaoui F., Kelly R.: A NSGA-II and NSGA-III comparison for solving an open shop scheduling problem with resource constraints. IFAC, International Federation of Automatic Control, 2016 s. 1272–1277.
[8] Delbem A. C. B., Carvalho A. C. P. L. F., Bretas N. G.: Main chain representation for evolutionary algorithms applied to distribution system reconfiguration. IEEE Trans. Power Systems, vol. 20, no. 1, Feb. 2015, pp. 425-436.
[9] Gawluk A.: Kierunki inwestowania a straty energii elektrycznej w sieci rozdzielczej. Przegląd Elektrotechniczny issue 3/2017.
[10] Guohua Fang, Wei Guo, Xianfeng Huang, Xinyi Si, Fei Yang, Qian Luo, Ke Yan: A New Multi-objective Optimization Algorithm: MOAFSA and its Application. Przegląd Elektrotechniczny, R. 88 issue 9b/2012, p. 172-176.
[11] Helt P., Parol M., Piotrowski P.: Metody sztucznej inteligencji – przykłady zastosowań w elektroenergetyce. Oficyna Wydawnicza Politechniki Warszawskiej, 2012.
[12] Hong Y. Y., Ho S. Y.: Determination of network configuration considering multiobjective in distribution systems using genetic algorithms. IEEE Trans. Power Systems, 2005. – Vol. 20. – No.2– p. 1062–1069.
[13] Kamrat W.: Metody oceny efektywności inwestowania w elektroenergetyce, Monografia Wydawnictwo PAN, Warsaw, 2004.
[14] Kamrat W.: Selected information technology tools supporting for maintenance and operation management electrical grids, Bulletin of the Polish Academy of Sciences-Technical Sciences, 2021.
[15] Kamrat W.: Selected problems of decision making modelling in power engineering, Sustainable Energy Technologies and Assessments, 2021
[16] Khushalani S., Solanki, J.M., Schulz, N.N.: Optimized Restoration of Unbalanced Distribution Systems. IEEE Transactions on Power Systems, no. 22, Issue 2. 2017, pp. 624-630.
[17] Kumar Y., Das, B., Sharma, J.: Multiobjective, Multiconstraint Service Restoration of Electric Power Distribution System With Priority Customers. IEEE Transactions on Power Delivery, no. 23, Issue 1, 2008, p. 261-270.
[18] Machowski J., Kacejko P., Robak S., Miller P., Wancerz M.: Badania systemów elektroenergetycznych w planowaniu rozwoju. Część 2. Analizy dynamiczne. “Wiadomości Elektrotechniczne,” vol. LXXXI, p. 3 -12, issue 8/2013, 2013.
[19] Marzecki J., Drab M.: Obciążenia i rozpływy mocy w sieci terenowej średniego napięcia-wybrane problemy. Przegląd Elektrotechniczny, R.91, p. 192-195, February, Issue 2, 2015.
[20] Marzecki J.: Modernization and development directions of low and medium voltage rural network, Przegląd Elektrotechniczny, 2019, vol. 95, s.67-70.
[21] Nita W.: Optymalne planowanie przebudowy elektroenergetycznych terenowych sieci dystrybucyjnych SN za pomocą metod ewolucyjnych, Doctoral Dissertation, Kielce University of Technology, 2020.
[22] Nita W., Filipiak S.: Planowanie przebudowy terenowych sieci dystrybucyjnych SN metodami ewolucyjnymi. Przegląd Elektrotechniczny, p. 92-98, Issue 4/2021.
[23] Nita W., Filipiak S.: Optimization of the reliability of power electric distribution grids MV with the use of heuristic algorithms. Przegląd Elektrotechniczny, p. 50-56, R. 98, ISSUE 6/2022.
[24] Ouyang, W.& Cheng, H.& Zhang, X.& Yao, L.& Bazargan, M.: Distribution network planning considering distributed generation by genetic algorithm combined with graph theory, Electric Power Components Systems, vol. 38, 3, 2019, p.325-339.
[25] Parol M: Analiza wskaźników dotyczących przerw w dostarczaniu energii elektrycznej na poziomie sieci dystrybucyjnych. Przegląd Elektrotechniczny, p. 122-126, Issue 8/2014.
[26] Parol M., Baczyński D., Brożek J.: Optimisation of Urban MV Multi-Loop Electric Power Distribution Networks Structure by Means of Artificial Intelligence Methods, Control and Cybernetics, 2012, vol. 41 (2012), p.667-689.
[27] Pijarski P.: Optymalizacja heurystyczna w ocenie warunków pracy i planowaniu rozwoju systemu elektroenergetycznego. Monografia, Wydawnictwo Politechniki Lubelskiej, Lublin 2019
[28] Pijarski P, Kacejko P.: A new metaheuristic optimization method: the algorithm of the innovative gunner (AIG). Engineering Optimization.- 2019, vol. 51, nr 12, s. 2049-2068.
[29] Pijarski P, Kacejko P., Miller P.: Advanced Optimisation and Forecasting Methods in Power Engineering—Introduction to the Special Issue. Energies 2023, vol. 16, nr 6, s. 1-20,
[30] Sowiński J.: Forecasting of electricity demand in the region, January 2019E3S Web of Conferences, International Scientific Conference on Electric Power Engineering DOI:10.1051/e3sconf/20198401010.
[31] Sowiński J.: Forecast of electricity supply using adaptive neuro-fuzzy inference system, May 2017, Conference: 2017 18th International Scientific Conference on Electric Power Engineering (EPE), DOI:10.1109/EPE.2017.7967248,
[32] Sowiński J.: Use of load volatility description in modelling of energy balance in the section “electricity supply,” January 2017, Rynek Energii 128, p. 35-39.
Autorzy: dr inż. Wojciech Nita, PGE Dystrybucja S.A. Oddział Skarżysko-Kamienna, dr hab. inż. Sylwester Filipiak prof. PŚk, Politechnika Świętokrzyska w Kielcach, Katedra Elektrotechniki Przemysłowej i Automatyki, E-mail: filipiak@tu.kielce.pl
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 99 NR 11/2023. doi:10.15199/48.2023.11.05