Published by Igor Razzhivin, Aleksey Suvorov, Mikhail Andreev, Aleksandr Gusev, Tomsk Polytechnic University
Abstract. The stability of electric power systems is one of its most important properties. This article discusses small-disturbance rotor angle stability: aperiodic and oscillatory. The authors consider, typically for stability analysis, the numerical integration methods by modeling in known numerous digital software simulation tools and propose a method for validating of simulation results by benchmark tool instead of field data. The feasibility of the proposed approach is clearly illustrated by the given fragments of the corresponding experimental studies.
Streszczenie. Stabilność systemów elektroenergetycznych jest jedną z jego najważniejszych właściwości. W artykule omówiono stabilność kątową wirnika o małych zakłóceniach: aperiodyczną i oscylacyjną. Autorzy rozważają, typowo dla analizy stabilności, metody integracji numerycznej poprzez modelowanie w znanych licznych narzędziach do symulacji oprogramowania cyfrowego i proponują metodę walidacji wyników symulacji za pomocą narzędzia wzorcowego zamiast danych terenowych. Wykonalność proponowanego podejścia wyraźnie ilustrują podane fragmenty odpowiednich badań eksperymentaln. (Walidacja aperiodycznych i oscylacyjnych obliczeń stabilności w praktycznych układach elektroenergetycznych)
Keyword: aperiodic and oscillatory stability, electric power system, simulation, validation.
Słowa kluczowe: stabilnośc systemu elektroenergetycznego, oscylacje, walidacja
Introduction
The stability of electric power systems (EPS) is one of its most important properties. The systematic basis for classifying power system stability was developed into appropriate categories by the CIGRE Study Committee 38 and the IEEE Power System Dynamic Performance Committee, according to which the stability is determined by the main system variable in which the instability can be observed and the size of the disturbance considered [1]. This article deals with the small-disturbance rotor angle stability that in the result can be of two forms: the increase in the rotor angle through a nonoscillatory or aperiodic mode due to the lack of synchronizing torque, or rotor oscillations of increasing amplitude due to the lack of sufficient damping torque.
In general the rotor angle stability problem involves the study of the electromechanical oscillations inherent is extremely important and relevant given the fact that modern EPS are constantly being updated: continuing growth in interconnections, the use of new technologies and controls, and the increased operation in highly stressed conditions. All of these have a significant effect on the properties of EPS. Therefore, with prospective and detailed design, the development of special automatic control devices, changes in EPS operating conditions, etc., its ability to regain a state of operating equilibrium is checked, that is the keep of stability. The aperiodic stability is associated with a change in the active power balance in EPS, the system must restore equilibrium between the electromagnetic torque and the mechanical torque of each synchronous machine in the system. Otherwise, the perturbation will increase the angle δ, as a result, the machine may fall out of synchronism.
Oscillatory stability is associated with the settings of automatic voltage regulators (AVR) of generators, since in some combinations of the circuit state condition and settings of excitation regulators, fluctuations in the control system can occur, causing increasing fluctuations in the angle δ until the machine drops out of synchronism [2, 3].
There are different approaches in estimating the static stability of EPS [4, 5], qualitative methods are widely used, for example, the use of Lyapunov functions, estimating the eigenvalues of the matrix. However, finding a suitable Lyapunov function has always been a difficult task, requiring significant mathematical calculations and transformations [6, 7]. Therefore, it is usually analyzed using numerical integration methods by modeling in numerous well-known digital software modeling (ST) tools, for example, Eurostag, PSS\E, ETAP, DIgSilent PowerFactory and ect. [8]. The authors [9] describe in detail the fundamental problems of numerical methods for solving differential equations, show that in this regard there is a problem of obtaining reliable modeling information that is inherent in all ST for calculating EPS modes, as a result of which the reliability of such calculations is often unsatisfactory.
Thus, the use of mathematical simulation results, with the unknown completeness and reliability of information about modes and processes in EPS, can lead to incorrect design and operational solutions related to the analysis of EPS dynamic stability, and the development of events and means for its preservation and improvement. This necessitates validation of such information [9]. It is obvious that in general, the validation of the calculation of modes and processes in EPS should be carried out using full-scale measurement data. However, the published results of the validation demonstrate the differences between the obtained process information in EPS and the full-scale data, which confirms the existence of the above problem of numerical modeling of large EPS. The authors in [10] described challenges related to existing validation approaches, in which the problem of mismatch of simulation results in ST is solved by adapting the calculation results to full-scale data by varying model parameters, mainly static characteristics of loads and regulators. It is important to understand that this approach allows you to adapt the model to a specific disturbance, but also does not solve the problem of comprehensive validation [11].
The article proposes an alternative approach to comprehensive validation of the calculation of aperiodic and oscillatory stability of EPS, based on the use of data modeling from benchmark tool (BT) as the source information, instead of full-scale data. An article is devoted to this issue, which is organized as follows: Methodology of comprehensive validation of ST describes the proposed approach to comprehensive validation of EPS stability calculations. Case studies presents the results of pilot studies confirming the feasibility of the proposed approach. The conclusions summarize the main findings.
Methodology of comprehensive validation of ST
To perform a comprehensive validation of ST calculation of the aperiodic and oscillatory stability of EPS as a source of the complete and reliable information, a model standard is attached – created on the basis of the Hybrid Real-Time Power System Simulator (HRTSim), which provides the non-compositional reproduction of a single continuous spectrum of normal and abnormal quasi-stable and transient processes in real time over an unlimited interval with the guaranteed acceptable accuracy in a particular equipment and simulated three-phase EPS in general [10, 12]. The validation of a BT created on the basis of HRTSim can be performed according to any state or process, for example, according to a quasi-stable one obtained using SCADA. Since the HRTSim uses the same detailed mathematical model EPS for all states and processes and uses a methodically accurate solution method. Therefore, the validation of one state can be guaranteed to extend to the entire spectrum and transients, including switching overvoltage. Thus, given the HRTSim properties, it can be used as a BT. Accordingly, a comprehensive validation of ST technique is proposed in the small-disturbance rotor angle stability, which is determined by a sequence of actions:
1. Setting and reproducing the circuit state condition and validating the reproduced data.
On the basis of the normal electrical scheme of a specific EPS and its database of equipment parameters and process automation settings in HRTSim and validating ST, within its capabilities, the initial circuit state condition of the simulated EPS is reproduced (if there are data from measuring devices of the simulated EPS, the possibility of using this information is not excluded). In the absence of some simulation data, their automatic calculation is carried out, based on the equations of current balances, active and reactive powers in adjacent nodes, taking into account power losses and voltage drops in transmission lines, transformers. Thus, the original circuit state condition of the simulated EPS is set.
The next step is the data validation, which is based on the evaluation of reliability of circuit state condition parameters of EPS model reproduction: current and power balances in nodes, state of switching equipment, the validity of active and reactive power values, currents and voltages in power lines and transformers. Based on the results of checking the validity of the PMU/SCADA data and detecting errors, they are automatically corrected.
2. Formation and implementation of validation scenarios.
To implement scenarios to evaluate the small-disturbance rotor angle stability of the simulated EPS, it is necessary and sufficient to reproduce a number of perturbations that can lead to aperiodic or oscillatory loss of stability. Due to the variety of factors, conditions and processes leading to the violation of the rotor angle stability, their complete validation is the subject of separate studies. Usually, the validation scenario for assessing the reliability of calculations of steady-state operation used to determine the aperiodic stability limit consists in load power increase representing the same increase in the generation and consumption of active power. In this case, generators mutual angles, the angles between voltage vectors at the terminals of study area are controlled.
The validation scenario for assessing the reliability of the calculations of transients used to determine oscillatory instability is focused on the most significant analysis currently associated with the work of automatic control systems: AVR with Power System Stabilizer (AVR with PSS), as well as frequency and power. This analysis can be performed either by methods of the automatic control theory or by the results of calculation of a transient process at small disturbances [4]. Due to the inapplicability of classical mathematical methods of the automatic control theory to evaluate the oscillatory instability of real EPS, this assessment is carried out based on the results of calculation on ST of the corresponding transients caused by small perturbations. For this purpose in states close to limit values of internal angles of synchronous machines taking into account the standard margin, load changes are created, leading to changes of mutual angles of generators (10-30 deg.). The evaluation of the oscillatory instability is carried out by waveforms of changes in mutual angles, the excitation voltage, the active and reactive power (RP), the frequency and voltage of the stator of synchronous machines.
Case studies
Experimental studies were carried out according to the proposed methodology. As the ST adopted common in the world practice the complex calculation state and electromechanical processes to EPS. A real three-phase normal electrical circuit of the Tomsk region was adopted as a model of the power system. The problem of obtaining the parameters of the real power system is widely known; moreover, the data in the power system is constantly changing. Therefore, it is not always successful to compare the operating mode of a real power system with a ST. In our case, the parameters of all models, all network elements of the simulated EPS, are set based from the data of dispatcher measurements, the configuration is set on the basis of the dispatch diagram. The electrical machines (EM) parameters, their excitation systems with AVR and PSS and prime movers, taking into account their control systems, as well as the characteristics of the mechanisms driven by electric motors, are set averaged according to the corresponding reference data. The transmission lines parameters mutual induction, the automatic control system laws of controlled shunt reactors and the characteristics of the magnetization of transformers (autotransformers) and EM are set similarly. The model includes 200 three-phase units, 42 electrical machines, 42 transformers, 97 transmission lines, 63 loads. At the first stage, the actual validation of the BT – HRTSim with SCADA was performed, the results showed a high level of coincidence. Also quasisteady-state compared process of short term electromagnetic transient as a result of which also get a good match [13]. At the second stage, a similar state of the all the EPS elements models and their parameters in the ST was formed as BT.
1. Validation of aperiodic instability
An intersystem transmission line of 500 kV was chosen as the investigated cross-section with a heavier state to assess the reliability of calculations of the aperiodic instability limit. Waveforms of the controlled operating variables in the critical stability state of the simulated EPS are shown in Figure 1.
According to the results presented, with the same load power increase, the processes calculated using ST and reproduced in BT (HRTSim) are fundamentally different and the violation of aperiodic instability in EPS in this experiment using ST is not detected. In fig. 1a, the waweforms of the δ angles demonstrates the rotation of all three EPS generators starting from 7 sec., then G2 and G3 are pulled into synchronism for about 8 sec., and G3 continues to asynchronous state. The HRTSim software (device) allows oscillographing the generators angles only in the range of 0 – 360 deg., therefore, discontinuities are visible on the graph. In fig. 1b, asynchronous state is not observed.

The results of their validation are presented in the table 1.
Table 1. Controlled operating variables in the critical state
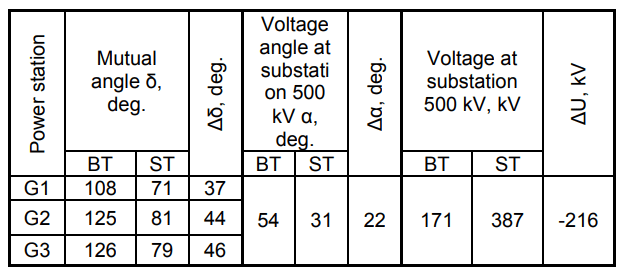
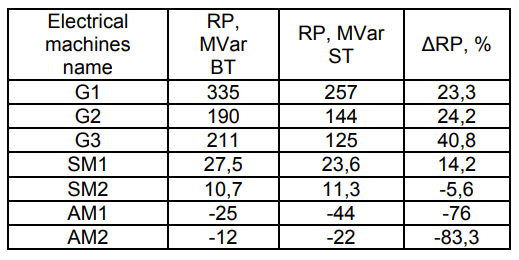
The greatest differences were obtained in the amplitude and phase of the voltage at the 500 kV substation and are caused by the discrepancy between the flux distribution of the PM in the network and the EM load by RP with their identical active power in the critical state and the initial steady-state (Table 2).
In particular, when the state becomes heavier, the loading of the generators according to RP occurs individually, in accordance with their sensitivity coefficients to various changes in the network, which significantly differ in static and dynamic modeling.
Table 2. Reactive powers of EM and their difference
2. Validation of oscillatory instability calculations
To determine the oscillatory instability, a 5% load power increase is performed on the PS. At the same time, for the monitored generator equipped with AVR with PSS, ST and BT (HRTSim) are initially set to the same average statistical AVR with PSS settings.
Figure 2 shows waveforms of the angle δ, voltage, and frequency, and excitation voltage, active and reactive power of the generator of one of the power plants.
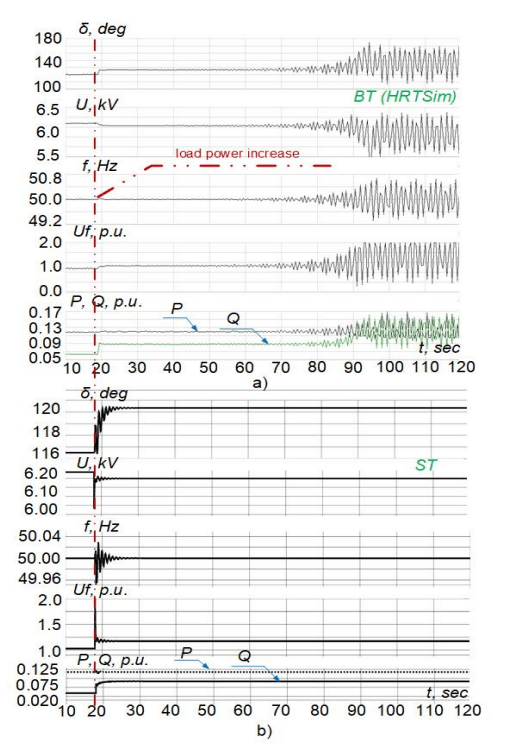
According HRTSim reproduced synchronous oscillation processes occur which are missing in similar waveforms obtained with ST for the following reasons:
1. The stator voltage of the generator on the ST waveform changes instantly with load power increase, due to simplified models of EM and network elements, therefore, the effect of AVR with PSS does not appear after the voltage drops to a level of ∆U = 0.18 kV, corresponding to a new flux distribution with a load power increase, and the corresponding the response of the main channel to the voltage deviation forms the excitation voltage of the critical value. Continuous operation of AVR with PSS in HRTSim contributes to a lower voltage drop at the generator terminals ∆U = 0.03 kV. Therefore, despite the identical mathematical models of automatic control systems in both means, in particular AVR with PSS, on the adequacy of which the results of the oscillatory instability assessment also depend, the completeness and reliability of the calculation of operating parameters, to a change in which automatic control systems respond, determine the nature of the course of transient processes, and, accordingly, the completeness and reliability of the assessment of oscillatory stability.
2. The influence of the transformer electromagnetic force (EMF) on the transient process of changing the variable equations of the stator voltage along the d and q axes is demonstrated by the waveforms presented in Figures 3.
The error in calculating the stator voltage along the d axis with the exclusion of the transformer EMF is associated with a large number of circuits along the d axis. The largest oscillation amplitude is characteristic of the transformer EMF, it mainly determines the transformation of oscillations between the rotor and stator circuits, leading to their occurrence in the stator voltage and the corresponding action of AVR with PSS, which contributes to the occurrence of synchronous oscillations of the generator. Therefore, the neglect of the transformer EMF leads to a significant distortion of transient processes reproduction at small disturbances, amplified by the incorrect functioning of automatic control systems, which does not allow, in most cases, to carry out a reliable assessment of oscillatory instability.

3. Significant and constant in magnitude inductive reactance of static network models elements for only one frequency value (50 Hz) distort the propagation of oscillations, especially low-frequency ones, which, together with a low probability of their occurrence in EM with their simplified modeling, significantly reduces the possibility of oscillations at small disturbances.
Conclusion
An alternative way for solving the problem of validation of calculations of small-disturbance rotor angle stability: aperiodic and oscillatory instability proposed, which consists in using the benchmark tool – HRTSim, as a source of initial data.
The results of experimental studies of the developed comprehensive validation ST tools in terms of calculating the aperiodic and oscillatory instability have confirmed the theoretically and practically grounded properties and capabilities of HRTSim, allowing for a guaranteed comprehensive validation of existing STs. The error in calculations of EPS aperiodic stability in ST is associated with inadequate EM loads on RP and its network flow distribution due to the use of static models. Validation of small-disturbance rotor angle stability calculations performed using ST revealed differences from processes reproduced using HRTSim, due to distortions of the generation and propagation of waveforms, especially low-frequency ones, associated with the simplification of EM models and the use of static models.
Acknowledgment – This work was supported by the Ministry of Science and Higher Education of the Russian Federation, project No. MK-3249.2021.4
REFERENCES
[1] Kundur P., Paserba J., Ajjarapu V., Andersson G., Bose A., Canizares C., Hatziargyriou N., Hill D., Stankovic A., Taylor C., Van Cutsen T. and Vittal V., Definition and classification of power system stability, IEEE Trans. Power Syst., 19 (2004), No. 3, 1387-1401, doi: 10.1109/TPWRS.2004.825981
[2] Komkov A. L. et al., Implementing the System Functions of the Automatic Proportional-Derivative Excitation Control of Synchronous Generators, Power Technol. Eng., 53 (2019), 356–359, doi:10.1007/s10749-019-01084-y.
[3] Hannan M. A. et al., Artificial Intelligent Based Damping Controller Optimization for the Multi-Machine Power System: A Review, IEEE Access, 6 (2018), 39574-39594, doi: 10.1109/ACCESS.2018.2855681.
[4] Kundur P., Power system stability and control. New York, NY, USA: McGraw-Hill, 1994
[5] Burghetti A. Handbook of electrical power system dynamics: Modeling, stability and control Canada: Institute of Electrical and Electronics Engineers, 2013
[6] Jastrzębski M., Kabziński J., Mosiołek P., Adaptive Motion Control with State Constraints Using Barrier Lyapunov Functions, Przegląd Elektrotechniczny, 92 (2016), No. 4, 112-119, doi:10.15199/48.2016.04.24
[7] Cifci A., Uyaroglu Y., Energy function analysis of a twomachine infinite-bus power system by Lyapunov’s second method, Przegląd Elektrotechniczny, 88 (2012), No. 2, 270-273
[8] Hatziargyriou N. et al., Definition and Classification of Power System Stability Revisited & Extended, IEEE Trans. Power Syst, doi: 10.1109/TPWRS.2020.3041774
[9] Guo H. et al., A critical review of cascading failure analysis and modeling of power system, Renewable and Sustainable Energy Reviews, 80(C) (2017), 9-22. doi:10.1016/j.rser.2017.05.206
[10] Suvorov A. et al., Comprehensive Validation of Transient Stability Calculations in Electric Power Systems and Hardware Software Tool for Its Implementation, IEEE Access, 8 (2020), 136071-136091, doi: 10.1109/ACCESS.2020.3011207
[11] Huang Z., Nguyen T., Kosterev D., Guttromson R., Model Validation of Power System Components Using Hybrid Dynamic Simulation, 2005/2006 IEEE/PES Transmission and Distribution Conference and Exhibition, Dallas, TX, USA, 2006,153-160, doi: 10.1109/TDC.2006.1668475
[12] Suvorov A. et al., Potential Application of HRTSim for Comprehensive Simulation of Large-Scale Power Systems with Distributed Generation, International Journal of Emerging Electric Power Systems, 20(5) (2019), doi: 10.1515/ijeeps2019-0075
[13] Suvorov A., Gusev A., Andreev M., Askarov A., A validation approach for short-circuit currents calculation in large-scale power systems, Int. Trans Electr Energ Syst., 30 (2020) No 4, e12276, doi: 10.1002/2050-7038.12276
Authors: PhD, senior lecturer of Department of Electric Power Systems, Igor Razzhivin, Tomsk Polytechnic University, 30, Lenin Avenue, Tomsk, Russia, E-mail: lionrash@tpu.ru; PhD, associate professor of Department of Electric Power Systems, Aleksey Suvorov, Tomsk Polytechnic University, 30, Lenin Avenue, Tomsk, Russia, E-mail: suvorovaa@tpu.ru; PhD, associate professor of Department of Electric Power Systems, Mikhail Andreev, Tomsk Polytechnic University, 30, Lenin Avenue, Tomsk, Russia, E-mail: andreevmv@tpu.ru; doctor of science, professor of Department of Electric Power Systems, Aleksander Gusev, Tomsk Polytechnic University, 30, Lenin Avenue, Tomsk, Russia, E-mail: gusev_as@tpu.ru
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 97 NR 6/2021. doi:10.15199/48.2021.06.26