Published by Piotr KAPLER, Warsaw University of Technology, Faculty of Electrical Engineering, Power Engineering Institute
Abstract. The article deals with minimizing the costs of electricity supply at the preliminary network planning stage. It presents selected information on costs in power engineering. The facility location problem and Mixed-Integer Linear Programming has been also described. A computational example of the application of this method is presented to solve the problem of minimizing the costs of electricity supply between high voltage / 110 kV power stations and 110 kV urban stations
Streszczenie. Artykuł dotyczy minimalizacji kosztów dostaw energii elektrycznej na etapie wstępnego planowania sieci. Przedstawiono w nim wybrane informacje dotyczące kosztów w elektroenergetyce. Opisano zagadnienie lokalizacji obiektów oraz metodę optymalizacji mieszanej całkowitoliczbowej liniowej. Zaprezentowano przykład obliczeniowy zastosowania tych metod do rozwiązania problemu zminimalizowania kosztów dostaw energii elektrycznej pomiędzy stacjami NN / 110 kV a stacjami miejskimi 110 kV. (Zastosowanie problemu lokalizacji obiektów do minimalizacji kosztów dostaw energii elektrycznej na etapie wstępnego planowania rozwoju sieci wysokiego napięcia).
Keywords: costs of electricity, costs minimizing, network development planning, mixed integer linear programming
Słowa kluczowe: koszty energii elektrycznej, minimalizacja kosztów, planowanie rozwoju sieci, optymalizacja mieszana.
Introduction
Electric Power System (EPS) consists of many interconnected elements whose purpose is the generation, transmission, distribution and usage of electricity. Simultaneously, it is a very important and strategic element of any area. Therefore, it is necessary that the decisions concerning power system taken at each stage of its design, operation or development, are optimal and reasonable. Thanks to this approach it should be possible to rationally manage energy sources, good operation of components as well as sustainable use of electricity by consumers both now and in the future.
Due to its complexity and large scale electric power system is a challenge for many optimization processes. Optimization tasks in this case can be both linear and nonlinear and have a large computational dimension. They are also accompanied by a number of different constraints, that must be maintained in order to model the correct operation of the power system. Often, the variables involved in the optimization process can be either integer or non-integer. Also some problems are NP-hard type. Optimization is proposed in each of the power system sectors: from generation to end consumers of electricity. Moreover, optimization may apply to both planned and already existing power infrastructure. Usually time horizon of optimization can be middle (2-5 years) or long term (10-20 years). The network planning process itself sometime takes into account the conditions of risk [1], uncertainty [2] or a probabilistic approach [3]. Factors encouraging the development are: an increase in power demand, the location of a new generation sources, access to fuels or increasing reliability of supplies [4].
This article is devoted to the minimization of electricity supply costs by application of facility location problem. Described situation occurs at the stage of preliminary high voltage (HV) network planning with usage of mixed integer linear optimization. The initial part of article presents selected issues about costs in power engineering. Also a description of the optimization method used is provided. The calculation part of article presents an example of minimizing the costs of electricity supply between potentially planned high voltage / 110 kV power stations and 110 kV urban stations. The final part of the article contains a summary and conclusions.
Selected issues concerning the costs of electricity supply
The operation of the power system is based on continuous coverage of the variable power demand of end users. Electricity, by its nature, cannot be stored easily and cheaply at present. At the same time, its production and transmission are associated with significant costs. These premises encourage rational management of electricity.
The supply of electricity is possible by building an appropriate infrastructure consisting of lines and power stations. The financial outlays for these investments are very large. In addition, it is also necessary to earn money on the provision of transmission services and collect funds for the ongoing operation and renovation works. In the future, investments in further network development may be required. Money can be obtained due to the difference between the total revenues that arose from the sale of goods or services and the total costs that had to be incurred in producing those goods and services.
In the case of power lines, expenditure on their construction is related with the length of the planned line, land charges and the use of specific technical solutions (for example types of poles or wires). It is estimated that the financial expenditure on the construction of a cable line is a multiple of 4 to 14 times the expenditure on the construction of an overhead line with the same rated voltage and length [5]. The operating costs result from the need to conduct qualified service work. Modifying the connections later on is cheaper and easier for overhead lines than for cable lines.
For power stations, investment outlays are related to the area where station is to be located, with the equipment used (for example circuit breakers or switch disconnectors) and the type of transformers. Operating costs will depend on the station layout used.
In addition, the transmission of electricity is accompanied by energy losses that must be paid for. Their values will depend on the length of the connections. They can be divided into load losses and idle losses.
Various methods are used in the electricity sector to determine fees for the provision of transmission services. The most popular include: the postage stamp method, the contract path method, the MW-mile method or method of tracing power flows. Each of the above methods give different outcomes as a result of the adopted assumptions and simplifications in their operation. The mentioned methods can be divided according to the way costs are treated. There are embedded cost methods and marginal cost methods. The first subgroup includes the postage stamp, contract paths and MW-mile methods. The second one is power flow tracing. Embedded costs deal with the power system as a whole and usage costs are borne by all users [6]. The marginal cost methods determine the value of the unit price to cover variable costs.
Linear mixed integer optimization and facility location problem
Linear programming has been used to solve optimization problems for many years. It is a special case of mathematical programming. Increased interest in this subject occurred at the turn of the 1950s and 1960s. Despite the fact that it is not new issue, nowadays it sill has a great application due to the development of computers and the application of possibilities for modern technical problems.
The idea behind this tool is to build a mathematical model that best reflects the characteristics of a real object as much as possible. Such a model is a record in the form of appropriate mathematical equations. The solution of the equations is the answer to the given decision problem. This approach helps making the final decision because building a mathematical model is cheap, simple and safe and does not require manipulating real objects.
In general, the linear programming problem can be defined in matrix form as (1):

subject to conditions (2) and (3):

where: z – objective function, c’ – matrix of objective function coefficients, A – matrix of limiting conditions coefficients, x – matrix of variables (unknowns), b – matrix of limiting values of the right side of the inequality (2). Formula (3) is a non-negative condition.
Each model consists of three basic elements. These are: the objective function (also known as the criterion function), decision variables and set of limiting conditions. The objective function is describing the goal to be pursued in the optimization task. This function is being minimized or maximized. It has a linear form. Decision variables are a description of resources related to the modelled issue. They are non-negative. The constraint conditions reflect the limits in the modelled process. They are described as inequalities with left sides containing linear functions.
Despite the simplicity of implementation, linear programming in its classic form is not always suitable for solving most optimization problems. It may turn out that in the description of the problem it will be necessary to include binary values (0 or 1) representing for example the existence or non-existence of a given object depending on certain conditions. In order to solve such problems, linear mixed integer optimization (MILP – Mixed Integer Linear Programming) is used. This approach applies if some (but not all) of the variables are binary.
In general, MILP problems can be defined identically using formula (1) and (2). However, condition (3) is replaced with condition (4).

where some variables are integer type and the rest are binary (0 or 1).
This type of approach is particularly useful for solving optimization problems in the power engineering industry, for example: the switching on or off generation units [7], designing distribution networks [8] or multistage planning of the development of the transmission network [9].
Optimization problems solved with the use of MILP must meet the following simplifying assumption: the share of each of the variables in the objective function is proportional to this variable and, at the same time, independent of the values of other variables in the task. Additionally, the values of constraints and decision variables must be known before performing optimization calculations. Sometimes, however, these values are not known exactly because they were derived from a rough estimate. Their influence on the optimization result can be obtained by applying a sensitivity analysis.
The facility location problem is well-known in optimization theory. In general, it deals with selecting the best locations of facilities that will cover the given customers demand while minimizing the costs of transportation. The input data are: set of candidate facility locations F = {1,…,m}, set of customers C = {1,…,n}, a cost function and a distance function. Moreover, the cost function may contain not only information about the cost of delivery but also the cost of opening a given facility. The result of calculation is the assignment of all customers to all opened facilities. Optimization models with facility locational problem can also be extended with additional constraints like: availability of fuels, raw materials or cost of land. Further description of this problem can be found in [10,11].
There are many variations of this task. In presented solution the mentioned problem has a MILP form – opening (or not) a new facility is a binary value. The objective is to minimize the total costs which can be divided to costs of opening new high voltage / 110 kV power station and costs of supply (which are proportional to the distance between power station and customers).
Formulation of the optimization problem
The optimization problem concerned the issue of minimizing the cost of electricity supply at the stage of preliminary high voltage network planning. The solution was obtained with an application of facility locational problem for power system planning. In the presented case facilities were 4 potentially planned high voltage / 110 kV power stations while customers were 9 urban 110 kV power stations. Every customer station can be theoretically supplied by each of planned HV / 110 kV station. The aim of the task was to find such connections between power stations so that the cost of electricity supply was minimal while simultaneously covering the required demand for active power.
All 110 kV power stations were located at different distances from supplying stations so the delivery cost was also dissimilar. It was assumed that the transmission of electricity to all customers can take place without violating any technical limitations like voltage drops or long-term current carrying capacity. Furthermore, it was also assumed that the total active power in supply stations was equal to the demand of consumers (Case 1) or supply exceeds that demand (Case 2).
The objective function (minimizing the cost of electricity supply) was defined as follows (5):

subject to conditions (6), (7) and (8):
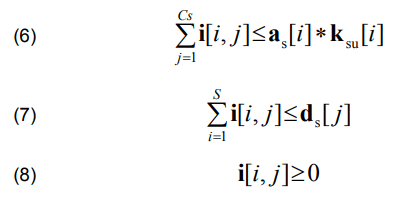
where: C – objective function constituting the cost of electricity supply subject to minimization, S – total number of power stations i, bs – the price of the building of the i-th power station, ksu – binary value related to the use of the station (0 – station not used, 1 – station used), es – cost of i-th station exploatation, c – delivery cost matrix for each station-customer pair, i – the amount of electricity transmitted from the i-th station to j-th customer, kl – power loss cost, Cs – total number of customers j, as – active power available at the station, ds – demand for active power at given customer.
In the objective function (5) it was taken into account that the cost of electricity supply from the HV / 110 kV to 110 kV stations will depend on the distance, active power demand, fixed cost related to the operation of a given high voltage station and the value of the charge for transmission power losses. Table 1 contains the values of the cost of delivery parameters for all potential station-customer pairs. They were created by applying the MW-mile method in which the delivery cost is defined by the formula (9) [12]:

where: Cdi – cost Energy supply, Pji – active power flow in the j-th line for the i-th transaction, Dj – length of the j-th line, Rj – required unit renewal value per line length.
The unit value of the renovation was 1.5% of the power line construction cost. The average price of building 1 km of high voltage lines was determined on the basis of data from [13]. The cost of construction of the high voltage / 110 kV power station was estimated at PLN 150 million (around 37 million euros). The costs of maintenance and repairs of each power station were assumed for 4% of capital expenditure [14].
Table 1. Energy supply costs form the MW-mile method, all values in PLN.
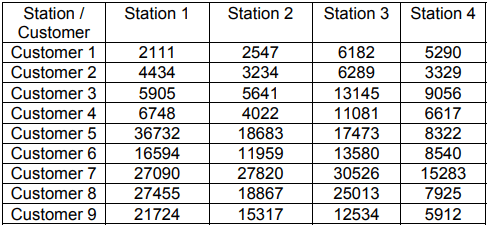
At the preliminary planning stage, it was assumed that all possible station-to-customer connections were taken into account. Some of these connections may later be rejected in further stages of network planning if it turns out that they are less optimal than others.
Solving the optimization problem
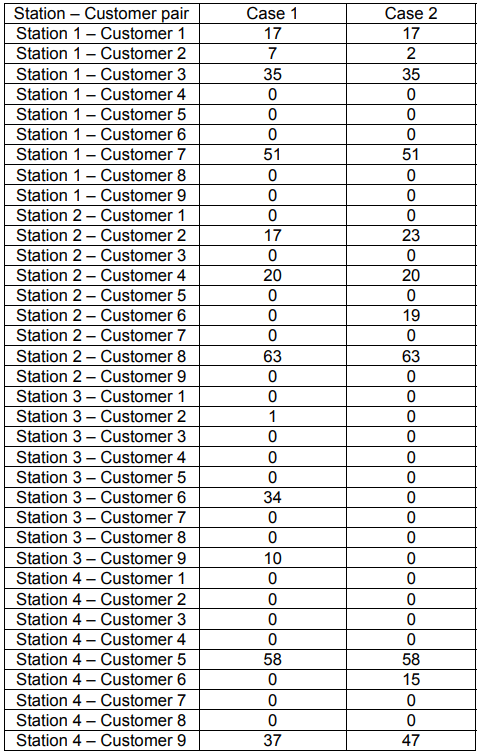
The task of minimizing the cost of electricity supply was solved in two cases. Case 1 assumed that the sum of active power in all power stations was equal to the sum of active power demand for all customers. In case 2, it was assumed that the planned total active power in all stations is greater than the customers demand. Table 3 presents the active powers in the stations for case 1 and case 2.
The solution of the problem was presented in the form station-customer pairs, for which, as a result of optimization calculations, active power values were allocated to cover the total demand at the customer (110 kV station) with the lowest possible cost of delivering and meeting additional conditions – expressed by the equations (6)-(8).
Table 4 shows binary values (1 or 0) corresponding to the necessity to build (or not) a given high voltage / 110 kV station in each of the cases. Table 5 contains the final summary of the results for both analysed cases. Where the connection of a given station with customer would not be optimal, the value of 0 appears. It is worth noting that connections with the value of 0 can be both in case 1 and case 2. This means that regardless of the values of available active power the given connection is not optimal.
Table 2. Demanded active powers, in MW
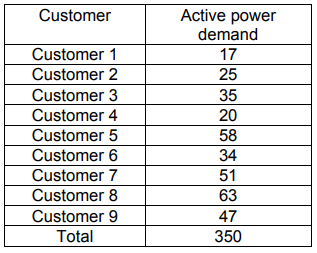
Table 3. Active powers in high voltage power stations, in MW
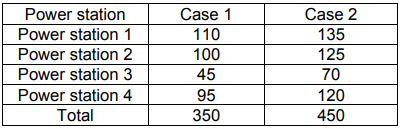
Based on the presented optimization results, the following values of the objective function (electricity supply cost) were obtained: for case 1 – PLN 650 244 922, and for case 2 – PLN 493 955 302. The result for case 2 is smaller because the calculations show that building of high voltage station 3 is redundant. Consequently, each Station 3 – customer pair has a 0 value in Table 5. Hence the result for case 2 is taken as an optimal for the considered planning problem.
Table 4. Binary values corresponding to the need to build a given power station in each case.

Table 5. Results of the optimization task solution, active powers in MW.
Summary and conclusions
The article presents an optimization task consisting in minimizing the costs of electricity supply at the stage of preliminary high voltage network planning. According to the conducted research, case 2 turned out to be more favourable than case 1. The objective function for case 2 is around 75% of the cost for case 1. However, the difference in cost values is PLN 156 289 620. This is more than the assumed construction price of the one high voltage / 110 kV power station.
The presented example relates to the situation when it is planned to transmit power form high voltage / 110 kV power stations to 110 kV stations located in a large urban agglomeration. In this case, the knowledge from the above analysis may be useful in further planning stages of the power network development for example, to the construction of load flow and short-circuit network models. The mentioned method may also be effective for making decisions concerning medium and low voltage network development. Due to the use of binary values, it can also be used to decide on the closing of existing power stations.
The results of the performed analysis depend on the input data used. It is necessary to choose the method by which the charges for transmitting electricity will be calculated. It is assumed that the price criteria used in the planning process should also take into account the problem of renewal of elements [15]. The second important factor is knowing the prices for the construction of the power line. The value of this price will strongly depend on many factors like type of line (overhead or cable) or the way it is located.
The advantage of the presented methodology using the mixed-integer approach is its efficiency, scalability and simplicity. The model used is universal and after introducing minor modifications it can be adopted to other optimization problems in the power engineering industry. Even if the obtained solution does not turn out to be fully satisfactory, it may constitute a starting point for the search of a new result. The disadvantage of an inaccurately conducted analysis may be both underinvestment and overinvestment in the transmission network [16]. Also, using the mixed-integer approach may be difficult due to possibly large number of binary (0,1) decision values.
When solving the problems of planning the power network development it is necessary to conduct multivariant analyses of various possible technical solutions. On this basis, it will be possible to further conclude whether it is worth implementing the intended investment or not. In the process of building decision models it is convenient to use, for example, linear programming. In addition, knowledge about the necessary investment outlays is also essential.
REFERENCES
[1] Marzecki J., Planowanie rozwoju miejskich Rozdzielczych Punktów Zasilających (RPZ) w warunkach ryzyka, Przegląd Elektrotechniczny, 90 (2014), nr. 2, 234-237
[2] Marzecki J., Planowanie rozwoju miejskich stacji 110 kV/SN w warunkach niepewności, Przegląd Elektrotechniczny, 96 (2020), nr. 1, 23-26
[3] Kubek P., Przygrodzki M., Wybrane aspekty wykorzystania elementów probabilistycznych w planowaniu rozwoju sieci przesyłowej, Przegląd Elektrotechniczny, 94 (2018), nr. 12, 108-111
[4] Gonen T., Electrical Power Transmission System Engineering: Analysis and Design, CRC Press, 2014
[5] Underground vs. Overhead: Power Line Installation-Cost Comparison and Mitigation, https://www.powergrid.com/2013/02/01/underground-vs-overhead-power – line-installation-cost-comparison/#gref (accessed 24.04.2020)
[6] Saganek D., Koszty wykorzystania elementów SEE w powiązaniu ze stanami pracy SEE – właściwości podejścia opartego na idei wpływu, Przegląd Elektrotechniczny, 91 (2015), nr. 5, 159-165
[7] Kamiński J., Kaszyński P., Mirowski T., Szurlej A., Krótkoterminowy matematyczny model systemu wytwarzania energii elektrycznej dla warunków Polski, Rynek Energii, czerwiec 2014
[8] Turkay B., Distribution System Planning Using Mixed Integer Programming, Elektrik, 6 (1998), nr. 1, 37-48
[9] Zhang H., Vittal V., Heydt G. T., J. Quintero, A mixed-integer linear programming approach for multi-stage securityconstrained transmission expansion planning, IEEE Transactions on Power Systems, 27 (2012), nr. 2, 1125-1133
[10] Dantzig G. B., Linear Programming and Extensions, Princeton University Press, Princeton, New Jersey, 1991
[11] E. Castillo, A. J. Conejo, P. Pedregal, R. Garcia, N. Alguacil, Building and Solving Mathematical Programming Models in Engineering and Science, John Willey and Sons, 2002
[12] Song Y-H. (edit), Modern Optimisation Techniques in Power Systems, Springer Science + Business Media, 1999
[13] Ciupak S., Linie WN na słupach kratowych vs linie WN na słupach rurowych, Konferencja Naukowo-Techniczna Elektroenergetyczne linie napowietrzne i kablowe wysokich i najwyższych napięć, Wisła 18-19.10.2017
[14] E. Dyka, I. Mróz-Radłowska, Ekonomia w Energetyce. Wybrane zagadnienia, Politechnika Łódzka, Łódź 2014.
[15] Einhorn M., Siddiqi R. (edit), Electricity Transmission Pricing and Technology, Kluwer Academic Publishers, 1996
[16] Dołęga W. Aspekty rynkowe planowania rozwoju sieciowej infrastruktury elektroenergetycznej, Energetyka, 8 (2015)
Author: Piotr Kapler, Ph. D., Warsaw University of Technology, Faculty of Electrical Engineering, Power Engineering Institute, Koszykowa 75, 00-662 Warsaw, Poland. E-mail: piotr.kapler@ien.pw.edu.pl
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 96 NR 11/2020. doi:10.15199/48.2020.11.35