Published by Shannon Edwards, Dave Bobick, and Steven Weinzierl, Radian Research, Inc.
Speaker: Steven Weinzierl, Radian Research, Inc., 3852 Fortune Drive, Lafayette, IN, 47905,
USA, Tel: (765) 449-5548, Email: stevew@radianresearch.com
Abstract: This paper compares and contrasts different methods to quantify VAR for single and polyphase energy meters. The results for the different methods will be compared in the presence of different realistic harmonic content scenarios, with sometimes a 30x difference seen in results between the methods. By understanding the differences between VAR methodologies in the presence of harmonics, we can take the next steps towards metrology consensus and standardization on how to measure and calculate them.
1. Introduction
As countries update their energy policy and infrastructure and increase investment in smart grid technologies, there is greater awareness of power and energy measurements. With that comes greater awareness of the increasing gap between consumed real power (watts) and generated apparent power (VA). Furthermore, as electronic devices become more sophisticated with increased semiconductor content, there is a rapid proliferation of highly non-resistive and nonlinear loads. In fact, many of these new non-resistive and non-linear devices are energy conserving devices such as dimmers, energy-efficient motors in new appliances, and compact fluorescent lights that are being deployed as part of the new energy policies.
Historically, reactive power (VAR) has been used to quantify the gap between consumed real power and generated apparent power of an AC electric power system [1]. Reactive power comes from 2 main sources:
1. Phase angle difference between the voltage and current sine waves, primarily due to non-resistive behavior such as device inductance or capacitance.
2. Waveform distortion from non-linear behavior, primarily due to harmonic content.
VAR is easy to determine in the first case of phase angle (non-resistive) contribution via a scaling factor of sin( ); therefore there is consensus among metrologists and measurement experts on how to quantify it.
However, VAR in the second case due to harmonic currents from non-linear loads is more complicated. Combined with the fact that reactive power in general does not transfer energy, there is a lack consensus amongst metrologists on how to measure and calculate VAR in the presence of harmonic content.
Ironically, the issue is further compounded by the observation that compared to older electromechanical meters, newer solid state meters have much smaller measurement error of active energy (watts) when supplied with active harmonic energy [2]. However, the solid state meters have shown widespread variation in VAR results, hence a call for “for an urgent international agreement” [2]. Because the utilities that produce energy need to build expensive base or peak generation plants based on VA and are beginning to charge consumers based on the VAR component, it is an important issue of fair commerce for a consensus to be achieved amongst metrologists.
This paper will:
• Compile and review the most common VAR calculations. 9 different ones are identified and discussed.
• Propose 6 representative waveforms (theoretical and actual recorded) with differing levels of harmonics in them to compare the results of the 9 different VAR calculations.
• Contributions from harmonics out to the 100th order are included.
• Compare the results of the 9 different VAR calculations across the 6 different representative waveforms.
• Make suggestions for next steps on how to proceed.
2. Compilation and review of best-known VAR calculations
Because there is no standardized nomenclature, the names for the methods were created by the authors and are now being used within the ANSI C12.24 committee.
The 9 identified VAR calculations are classified into 3 broad types:
Pure fundamental calculation appropriate for a pure sinusoidal which by definition includes the effects of only the first harmonic and discards contributions from higher harmonic orders.
Phase shift calculations. This category has 5 variants within it:
• Integral Phase Shift Method Fixed Frequency
• Integral Phase Shift Method Exact Frequency
• Differential Phase Shift Method
• Quarter Cycle Delay Method
• Cross Connected Phase Shift Method
Vector calculations. This category has 4 variants within it:
• Vector Method using VA RMS
• Vector Method using VA Average Responding
• Vector Method using VA RMS & Fundamental Waveforms
A glossary of symbols used in the formulae is given at the end of the paper.
2.1. Fundamental calculation
VARs for each element are calculated by multiplying the fundamental of the voltage times the fundamental of the current times the sine of the phase angle between them:
VARi = || Ṽi || ⋅ || Ĩi || sin(θi)
Where the fundamental RMS Voltage and Current are calculated:
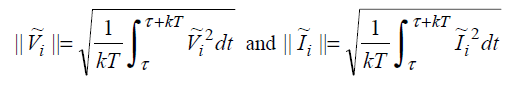
2.2. Phase shift VAR calculations
The genesis behind this calculation type is primarily historical: Early analog electromechanical meters could only measure active (real) watthours. By introducing a known reactive element (typically capacitor and resistor network) into the circuit to create a known 90° phase shift on the voltage axis, the watt-hour measurements of the meter could in essence be “tricked” into measuring the reactive component. The added reactive element made the reactive portion of the power active so the meter could measure it, and made the active part reactive to be invisible to the meter.
Once two sides (watts and VARs) of the power triangle are known, the third (VA) can be easily calculated from the power triangle as shown in Fig. 1 [3]:

While the phase shift method was a resourceful way to make the best use of available technology at the time, this method has shortcomings because the selection of the C and R values are frequency specific: Although the phase shift was correct, it would cause amplitude distortion as frequency changed. The proliferation of the phase-shift techniques was the result of future more sophisticated iterations of it to minimize its shortcomings.
Within the phase shift methods, there are integral (integration) methods and differential (differentiation) methods. The concept is based on:

I.e., integrating the voltage axis gives a 90° phase shift. Differentiation works in a similar manner. However:
• Integration attenuates the amplitude of the harmonics
• Differentiation amplifies the amplitude of the harmonics
• With both, the amplitude “distortion” is proportional to the frequency.
So while the phase shift was achieved, it was at the expense of amplitude distortion. These methods then renormalize the amplitude of the integrated (phase-shifted) voltage to create a voltage whose fundamental voltage would be identical in amplitude to the fundamental component of the voltage axis. Originally the frequency could not be measured in real time so a fixed value (60Hz or 50Hz as appropriate) was assumed; later the frequency was measured and used in the calculation or the equivalent R and C values were assigned adaptively in real time.
The equation for the “Integral Phase Shift Method Exact Frequency” method is:
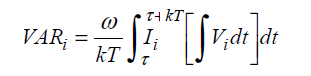
Substituting (2 ×60) or (2 ×50) as appropriate for gives the formula for “Integral Phase Shift Method Fixed Frequency”.
The equation for “Differential Phase Shift Method” is analogously:
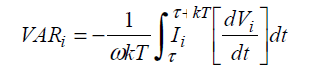
The “Quarter Cycle Delay Method” could be digitally implemented with charge-coupled devices to achieve the phase shifting. Its advantage over the earlier integral/differential phase shift methods is that it doesn’t impact the amplitude. Compared to the integration method, it appeared to periodically flip the sign of a given harmonic’s contribution, and so more often than not will make the VAR calculation be more negative. Its equation is:

Finally, the “Cross Connected Phase Shift Method” is based on creating a voltage that is 90° delayed from the voltage axis and adjusting the amplitude to match the amplitude of the voltage axis input. The 90° delay is created by subtracting the voltage phase that is 240° behind from the voltage phase that is 120° behind. The amplitude is then adjusted by dividing by √3. This phase shift and amplitude adjustment assumes that the voltages are balanced and spaced 120° apart. VARs for each element are calculated by multiplying the 90°-delayed amplitude-adjusted voltage times the current and integrating over the fundamental period:
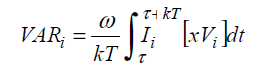
Where the 90° delayed and amplitude corrected voltages are:

This method has been used extensively in 3-phase electromechanical meters. Its biggest shortcomings are:
• The assumption of balanced voltages across the phases. This is rarely true, giving the wrong amplitude value in the calculation.
• The assumption that the voltage phases are exactly 120° apart (rarely true).
2.3. Vector VAR calculations
These methods are all based on measuring VA and Watts, and calculating VAR for each phase from the power triangle (Fig. 1):

where:

“VAR, Vector Method using VA RMS” uses the fundamental and all harmonics in the calculation:

and then substituting into Eq. 1 and Eq. 2.
“VAR, Vector Method using VA Average Responding” works similarly in concept to the Simpson meter with a D’Arsonval meter movement [4]. It’s worth a mention for historical reasons:
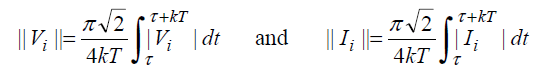
One artifact is that the calculated average responding VA can be less than the watts value, contradicting the power triangle shown in Fig. 1. This is because, for example, a voltage signal which is 0 for some time – as in the case of a dimmer – ends up with a low average value. Hence why the RMS method is better.
“VAR, Signed Vector Method using VA RMS, & Fundamental Waveforms” for polyphase meters attempts to prevent cancelling of signs of different harmonics by getting the sign correct with a multiplying factor of
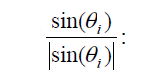
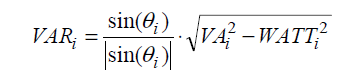
The rest of the equations are the same as for “VAR, Vector Method using VA RMS”. One practical and obvious difficulty with this method is when =0 and the signing factor blows up. L’Hôpital’s rule [5] must be invoked in real-time to determine which infinite value is smaller.
3. Waveforms
The six representative waveforms used to compare the results of the calculations consist of three theoretical ones and three actual ones recorded in the field. Their names and short descriptions are given here, with pictures of them in the following subsections:
Theoretical:
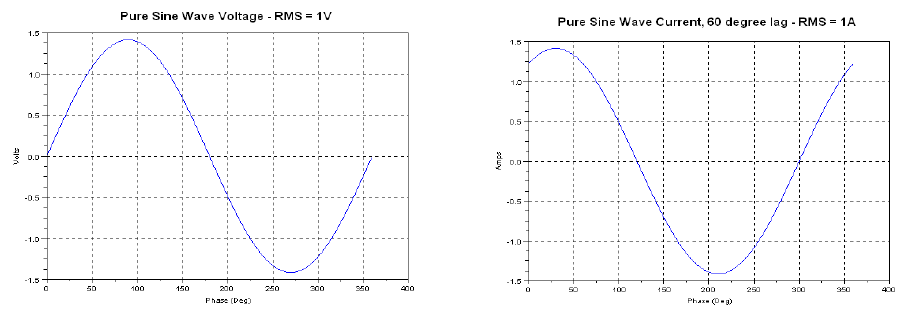
• Sine wave voltage, Sine wave current -60° lag. Current is lagging voltage, simulating an inductor present in the load. This waveform is used as a reality check – all VARs calculations should be scaled by sin(60°), or 0.866.
• Sine wave voltage, Phase dimming 90° conduction angle. This represents an energy-conscious consumer using a light dimmer at ½ power.
• Narrow Current Pulse. With the proliferation of switching and Pulse Width Modulated (PWM) power supplies [6], this type of waveform might be reflected back from the load to the line.
Actual ones: The National Research Council Canada (NRC) recorded actual waveforms (WF) at a variety of sites in the field; labeled them to anonymize them; archived them; and made them available upon request. While the waveforms may look unbelievable, they are indeed real. Using a digital frequency transformer, we parameterized them into harmonics components out to 100th order to run them through various closed-form VARs calculations given in Section 2.
• NRC WF23. Actual waveform recorded in the field. Its V and I waveforms are fairly symmetric, with the V waveform having smaller high frequency spikes and I waveform have larger amplitude, lower frequency harmonics.
• NRC WF139140. Actual waveform recorded in the field. Its V waveform is asymmetric, indicating the presence of more even harmonics.
• NRC WF13621363. Actual waveform recorded in the field. Its V waveform is mostly symmetric but has significant spikes and sags. The I waveform is nearly square, indicating many high order harmonics.
To better enable comparisons, all waveforms have been normalized to 1Vrms and 1Arms, i.e., 1VArms.





4. Results and discussion
A graphical summary of the results comparing the different VARs calculations for the different waveforms is given below:

Observations on the results for each of the waveforms are as follows:
Sine wave voltage, Sine wave current -60° lag. As expected and hoped, all VARs methods return the same value of 0.866, so this reality check is passed.
Sine wave voltage, Phase dimming 90° conduction angle.
• All integral phase shift methods gave the same value of 0.45088 because the voltage waveform used was a pure sine wave (no harmonics), i.e., || Ṽi ||= 0 in VARi = || Ṽi || ⋅ || Ĩi || sin(θi) for i 1.
• The vector methods gave noticeably higher values versus the phase-shift methods because the phase-shift methods miss the contributions of the harmonics.
• All the vector RMS methods gave identical values of 0.70539. However the vector average responding method was the clear outlier with a much lower value of 0.10101 because the voltage signal is 0 for an appreciable time, causing a lower average value.
Narrow Current Pulse. Similar comparison as the previous case of phase dimming:
• All integral phase shift methods gave the same value, but it’s 0 – they totally missed the energy. This is because the voltage waveform used was a pure sine wave (no harmonics), i.e., || Ṽi || = 0 for i 1.
• The vector methods gave noticeably higher values versus the integral methods – the integral methods were missing energy contributions from higher harmonics.
• All the vector RMS methods gave identical methods of 0.76571. The vector average responding method was again the clear outlier of the group with a much smaller value because the voltage signal is 0 for an appreciable time. In fact, its VAR value was imaginary because erroneously VA < Watt in the radical VAR = √VA2 – Watt2.
NRC WF23. The RMS vector methods show highest magnitude because they detect the higher harmonics on both the V and I axes. The differential phase shift method is noticeably lower, most likely because harmonics with negative signs got amplified by the differential phase-shift method and erroneously over-subtracted from the overall total. The vector average responding is lower because the I waveform is near zero for an appreciable time.
NRC WF139140. Here is a case with 30x differences between results. The phase-shift methods are erroneously lower because a pure voltage sine wave was assumed and they’re missing the contributions from the higher even harmonics. Again the differential phase-shift method is lower as it is likely amplifying a negative harmonic and over-subtracting its contribution.
NRC WF13621363. Finally, a case where there is disagreement between the vector VA RMS methods. VA RMS is by definition using all positive quantities, so in this case the “VAR, Signed Vector Method using VA RMS, & Fundamental Waveforms” (last green bar) accounts for contributions from negative harmonics and could be more correct.
5. Conclusions
Significant differences are seen in VAR results on a variety of waveforms. Differences are seen in both sign and order of magnitude, and the agreement gets worse as the harmonic content increases. Due to the proliferation of already-installed electric meters with the different VARs methods, suggesting or mandating a single standard method and then retrofitting the field is impractical. The best course of action is for manufacturers, utilities, and consumers to be aware of the differences and act accordingly.
The core issue is equity in billing in the presence of large harmonic content in both the voltage and current waveforms in the power grid. The power triangle (Eq. 1) only works for sinusoidal waveforms and so is no longer valid. Measuring real consumed power (watts) and reactive power (VARs) separately is in a sense a historical crutch which started out because the original meters could only measure real power.
The technology now exists to measure meter VA and VA-h at the point of use. While there still needs to be consensus among metrologists on VA measurements, that it much more likely to happen than achieving consensus on VAR measurements. Because VA is more directly related to actual cost of generation and more likely to achieve consensus on its measurement, it might make sense to start with VA and address VARs later.
6. Acknowledgements The authors gratefully acknowledge the excellent inputs from, and discussions with, the members of the ANSI C12.24 committee.
7. References
1. http://en.wikipedia.org/wiki/AC_power.
2. The Registration of Harmonic Power by Analog and Digital Power Meters, Johan Driesen, Thierry Van Craenenbroeck, and Daniel Van Dommelen, IEEE Transactions on Instrumentation and Measurement, vol. 47, no. 1, Feb. 1998, pp. 195-198.
3. Handbook for Electricity Metering, 10th edition, Edison Electric Institute, pp. 31-21, 2002.
4. http://en.wikipedia.org/wiki/Galvanometer.
5. http://en.wikipedia.org/wiki/L%27H%C3%B4pital%27s_rule.
6. http://en.wikipedia.org/wiki/Pulse-width_modulation.
8. Glossary
Index “i” represents the ith phase in the poly-phase network. i=1 single-phase, maximum i is 3 for three-phase.
Ṽi = Potential component fundamental (1st harmonic order)
Ĩi = Current component fundamental (1st harmonic order)
Ṽ(h)i = Potential component for harmonic order (h)
Ĩ(h)i = Current component for harmonic order (h)
(h)i = Phase angle of the potential for harmonic order (h)
(h)i = Phase angle of the current for harmonic order (h)
Vi = Generalized potential waveform (fundamental and all harmonics)
Ii = Generalized current waveform (fundamental and all harmonics)
i = Phase angle between the fundamental potential and current, (1)iminus (1)i
t = VAR-hour and VA-hour integration interval measured in seconds
T = Fundamental period
k = Number of fundamental periods
= Fundamental angular frequency = 2 f0, where f0 is the fundamental frequency
= Start time of integration
|| || = Generally represents the norm of the wave function: 1-norm (Average) or 2-norm RMS.
|X | = Absolute value of X
bVi = Blondel Theorem transformed Voltages
bV1 = V1 −V2 ,bV2 = 0 , bV3 =V3 −V2

Source: 2010 NCSL International Workshop and Symposium