Published by 1. Andriy CZABAN1, 2. Vitaliy LEVONIUK2, 3. Radosław FIGURA1,
Kazimierz Pulaski University of Technology and Humanities in Radom (1), Lviv National Agrarian University (2) ORCID: 1. – 0000-0002-4620-301X; 2. 0000-0003-2113-107X; ; 3. 0000-0001-8048-5623
Abstract. In this work, on the basis of an interdisciplinary method of modelling, a mathematical model of a power system is presented, main element of which system is an gas switch. For modelling of non-mechanical part, a popular theorem on flickering centre of speed of rotation was used. For a mathematical model of an arc, when the resistance was of non-linear nature, a resistive-capacitive alternative diagram was used. The final system of differential equations was presented in a normal cauche form. Results of simulation were given as drawings and were analysed.
Streszczenie. W pracy na podstawie interdyscyplinarnej metody modelowania zaproponowano model matematyczny układu elektroenergetycznego, głównym elementem którego wyłącznik gazowo-elektryczny typu SF6. Dla modelowania części mechanicznej wyłącznika wykorzystano słynny teoremat o migowym centrum prędkości obracania. Dla modelu matematycznego luku wykorzystano rezystancyjno-pojemnościowy schemat zastępczy, gdy rezystancja rozpatrywała się jako funkcja nieliniowa. Końcowy układ równań różniczkowych przedstawiony w normalnej postaci Causze’go. Wyniki symulacji komputerowej podano w postaci rysunków, które analizują się. (Model matematyczny wyłącznika wysokiego napięcia jako elementu układu elektroenergetycznego).
Keywords: high voltage switch, mathematical modelling, the Hamilton-Ostrogradskii principle, the Euler-Lagrange equation.
Słowa kluczowe: wyłącznik wysokiego napięcia, zasada Hamiltona-Ostrogradskiego, równania Eulera-Lagrange’a, nieustalone procesy.
Introduction
Analysis of unsteady electromagnetic processes of complex power systems is extremely important both at the design stage and during exploitation of the said systems, which are elements of one integrated power system.
It is obvious that such systems are characterized with very sophisticated physical processes, for the purpose of analysis of these it is necessary to use complex mathematical model, based on the theory of common differential equations, and sometimes on common equations and partial derivative equations.
Power systems consist of many various components. In order to provide highly adequate mathematical model it a must to describe each of the operating electric devices in details. Depending on the task, attention should be paid to a required device.
This work concentrates on one of the most crucial element of power systems of high voltage – the gas switch. In order to switch long power supply lines on/off, it is the said device that is used. In the course of analysis of unsteady processes of power supply line of high voltage, an important problem occurs, i.e. the necessity to model electric arc processes in switches of high voltage and high voltage. In a general case when current function curve breaks due to contacts opening, an arc is formed, physical principles of which arc are highly complex. These principles are described by plasma theory, electromagnetic field, thermodynamics theory etc. Nowadays, the models of these devices [1] are quite complex and cumbersome. Therefore they are not always acceptable in the analysis of transients in electrical networks.
Another factor to consider is the mechanical processes that occur in the switch when moving the contacts. These processes take as much time as the electromagnetic ones that occur in the switched elements of electrical networks, and therefore can affect the latter.
It is obvious that providing highly adequate mathematical model of the switch requires both use of complex theory and few experts.
Nowadays, SF6 circuit breakers ABB type LTB 362-800 (T) E4 are widely used for switching elements of ultra-high voltage electrical networks on the territory of European Union and in the CIS countries. These switches consist of two modules, each of which has two pairs of series-connected contacts – two fixed and two movable, which are driven by one mechanism for moving the contacts (see Fig. 1). Capacitors are connected in parallel to the contacts for even voltage distribution during switching.
Figure 2 presents proposed simplified kinematic diagram of right side of the mechanism triggering of switch’s contacts. Left side is symmetrical to the right one.
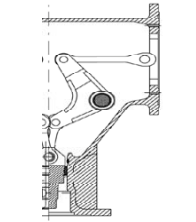

The mentioned mechanism of movement of contacts (see Fig. 1) consists of two crank mechanisms which are symmetrical concerning a longitudinal axis of the whole mechanism. The mechanism is driven by a spring (not shown). These crank mechanisms have a specific design, because the axis of movement of the spring and the axis of movement of the contacts do not coincide with the center of rotation of the mechanism itself. Such crank mechanisms are called deaxial.
We have already built a mathematical model of such a mechanism [2], however, with the high adequacy of this model, it is too cumbersome and difficult to implement as a computer program for the potential user. Therefore, in the present paper, we propose to use a mathematical model of the switch with a simplified kinematic substitution scheme for the analysis of transients in electrical networks with SF6 switches. A comparative analysis of the work of both models showed the convergence of the obtained results by 92%. This gives grounds for the application of a simplified substitution scheme when the calculations do not require high accuracy. The use of a simplified kinematic substitution scheme does not significantly affect the adequacy of the results, but allows to significantly simplify the model of the switch.
In this article, on the basis of variational approaches, we will build a mathematical model of the electrical network, the main element of which is a switch. This approach makes it possible to avoid the decomposition of a unified dynamic system and to obtain the initial equations of the electromagnetic and mechanical state exclusively from a unified energy approach, by constructing an extended Lagrange function [3].
Recent research analysis
Power system problems are often discussed in scientific articles, there are plenty of alike works. Work [4] provides analysis of problems concerning design of mathematical models and macro models of power supply lines with switches. The mathematical model here is developed in the MatLab/Simulink software package. Obtained results are presented.
In [5], the study of electromagnetic transients during the shutdown of short-circuit currents on the 500 kV transmission line with shunt reactors turned on is presented. Here, the model of the switch and other elements of the electrical network is built in the EMTP-RV software package.
In [6] shows the results of researches of the reasons of accidents of SF6 switches during switchings of the compensated power lines of 750 kV. Based on the simulation model developed in the MatLab/Simulink software package, the study of electromagnetic processes in compensated power lines depending on the switching moments is carried out.
In [7] the influence of transient switching processes in power lines on the operational state of the power system was studied. In [8] the transient electromagnetic processes in the power line with shunt reactors during an emergency shutdown due to a short circuit were analyzed. In these works, the study was also carried out in the software package EMTP-RV.
Analysis of the above mentioned works, and numerous articles, make us judge that their authors in the course of modeling transient electromagnetic states neglect mechanical processes in high voltage switches, which are commensurate in duration with electromagnetic, and therefore can affect them. We also see that in the present time the most popular software packages for the study of switching processes are MatLab and EMTP. However, in these systems, the switches are modeled in such a way that the break in the function of the circuit breaker current occurs exclusively at zero, which is not always true.
Based on the above, the aim of this work is a developing of a mathematical model of the ultra-high voltage switch taking into account the simplified kinematic scheme of replacement of the mechanism of moving its contacts to simplify the switch model and analysis of switching transients in electrical network elements.
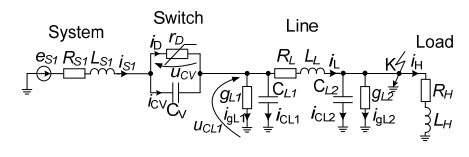
Mathematical model of the system
Figure 3 shows part of power grid of high voltage, which part consists of power system (EMF), internal resistance, inductance, high voltage switch, the latest presented as nonlinear active-capacitive components connection, П-alternative diagram of power supply line with concentrated parameters and resistive-inductive load.
We propose to use variational principles for building of mathematical models of electrical network elements, in particular the modified Hamilton-Ostrogradsky principle [3].
For the system we study, the extended action functional by Hamilton-Ostrogradski and its variation will be the following [3]:

where S is the action by Hamilton-Ostrograd, L* is the augmented Lagrange function.
Expanded lagrangian of the integrated system is given as follows [3]:
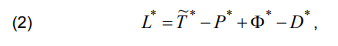
where Т~* – kinetic coenergy, P* – potential energy, Φ* – energy dissipation, D* – energy of outside nonpotential forces.
Next, elements of dispersed expanded non-conservative lagrangian is presented:
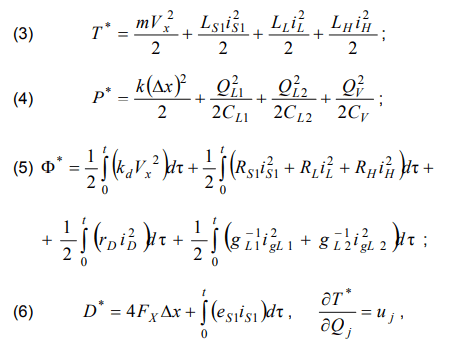
where LS1, LН, LL – system inductances; RS1, RН, RL – system resistances; eS1 – electromotive force; СL1, CL2 – line’s capacities; gL1, gL2 – line’s conductivities; iS1, iН, iL, igL1, igL2 – currents; CV – capacity of contacts capacitor; rD – non-linear resistance of arc; iD – arc’s current; ∆х – spring’s end shift; Vx – spring’s end speed; k – resilience coefficient; kd – spring diffusion coefficient; m – contacts mass reduced to a spring system; FX – arc displacement force reduced to a spring system; Qj – charge of the j-th element; uj – the voltage of the j-th element.
For example, we present a differential equation that describes the transient process of current in an equivalent power system (System, see Fig. 3) based on the principles of variation.
We write the Euler – Lagrange equation [3]
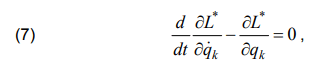
where q is the generalizing coordinate; q̇ – the speed of the generalizing coordinate. As a generalizing coordinate we take the charge – the speed of the generalizing coordinate
qS1 = QS1, q̇S1 = dqS1/dt = dQS1/dt = iS1.
We should note that in the Euler-Lagrange equation (7) we substitute only the components that relate to the element for which we obtain the equation of the electromagnetic state, since the derivatives of other functions (generalized coordinates) are identically zero, because the latter is not differentiated.
We write the Euler – Lagrange equation (7) taking into account (3) – (6) given that
∂Т* / ∂QS1= uV – uCL1.
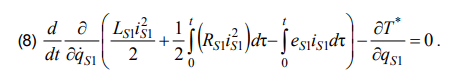
We obtain the equation of the extremals of the Hamilton action functional by changing the order of differentiation (8) and applying the theorem on the derivative of the integral over the upper bound:
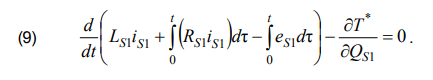
This way we obtain an equation that describes the current of an equivalent power system:
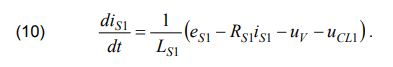
In order to avoid overloading the article with mathematical inferences, we will not reflect the procedure for obtaining the rest of the equations, but only present their final form. You can learn more about the principles of obtaining the equations of such a prolan, for example, in [3, 9]
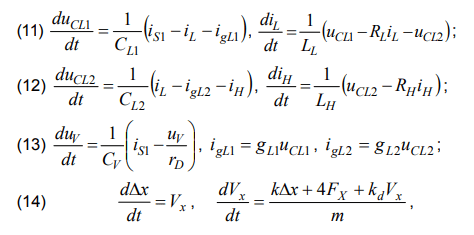
where igL1, igL2 – line leakage; uCL1, uCL2 – line start voltage, line end voltage; uV – voltage between the contacts.
As already mentioned, electric arc resistance rD is nonlinear and it depends on distance between contacts. In order to describe this resistance, it is necessary to know how the resistance is related regarding contacts distance.
On the basis of Fig. 2, the equation takes the following form:
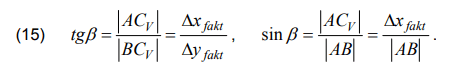
Then, referring to the popular theorem on flickering centre of speed, the equation is [10]:

On the base (15) and (16) the Vx is calculated by formula:

Using (15), angle β is calculated:

Next, putting (18) into (17) Vy speed is calculated:
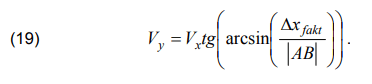
Differential equations for finding speed increase will be obtained Δyfakt

On the basis of Fig. 2, equations for finding functions Δy and Δxfakt are made

In a general case, resistance rD is of exponential nature [11].
Therefore approximation is done using 5-degree polynomial:
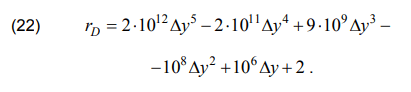
Dependence (22) initially has a slowly increasing character (simulates arc combustion), and when the contacts diverge by a distance of more than 0.02 m – a sharply increasing nonlinear character (simulates arc attenuation).
Integration is calculated for differential equations: (10) – (12), first equation in (13), (14), (20). This is due to the following second and third equations in (13), (19), (21), (22).
Computer simulation results
Computer simulation of transient states was carried out for power supply line presented in Fig. 3, mechanical processes in high voltage switch of type ABB LTB 362-800 (T) E4 were calculated.
The experience proceeded as follows. The system startup was realised by activating EMF. After reaching transient state (0,18 s) in p. К, symmetrical 3-phase short circuit was triggered. Next, in 0.04 s (time for activation up of relays protection) contacts started to disconnect. The system parameters were: eS1 = 612sin(ωt + 20°) kV, RS1 = 2,032 Ω, LS1 = 0,161 H, RL = 6,85 Ω, LL = 0,333 H, CL1 = CL2 = 0,0000024 F, gL1 = gL2 = 0,0000058 Sm, CV = 400·10-12 F, LH = 0,7 H, RH = 800 Ω, k = 320000 N/m, m = 2,032 kg, kd = 0 Ns/m. The following assumption was adopted: FX = 0 N (arc displacement force not referred to).

Temporary switch current values are shown at Figure 4. Analysis of the figure let one conclude that for short circuit the surge current is over 7 times higher. Within this time interval, protection system got activated up. Next due to switch operation, the current began to actively drop down and in 0.3 seconds its value was zero. The line got disconnected.
In Fig. 5, voltage between switch’s contacts was presented. It is obvious that in an operating state of the system the voltage value is zero. Next, in the switch activation state, the voltage increases to 750 kV. With contacts disconnection resistance grows, in 0.03 s voltage on contacts equals EMF rated voltage, 630 kV.
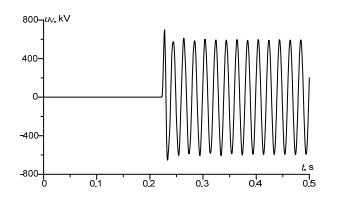
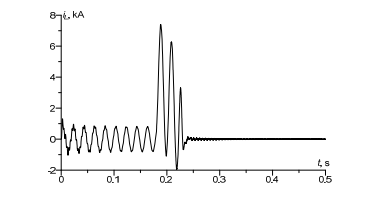
In Figure 6 transient current in power supply line is presented. It can be observed that in operating state of the system, the maximum current value was 0.9 kА, in short circuit state it was 7 kА. When comparing Figures 4 and 6, a difference is observed, the difference may be a result of complex processes occurring on the line end.
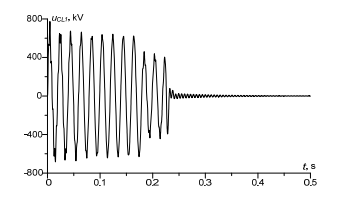
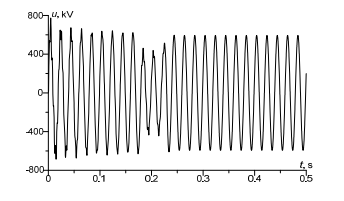
Figures 7 and 8 are very interesting, they visualize voltage on the right and on the left of the switch. Analysis of the figures leads to the following conclusion: after short circuit on the line end (p. K),the voltage on the line start dropped to 400 kV. After activation/of the switch, voltage on the right dropped down to zero (Fig. 7). As for the second figure (Fig. 8), the case is different. Voltage in a transient state equals system’s EMF.

Transient disconnection of switch’s contacts within time interval [0,2; 0,28] s shows at Fig. 9. This drawing can be treated as a light theme of this work concept. The approximated curve shows the dependence of arc resistance as a function of the distance of contacts and time. It has been described in the present paper by a mathematical model. This model takes into account the elements that make up the high-voltage circuit breaker.
Conclusions
1. The use of the modified Hamilton-Ostrograd principle gives the possibility to build mathematical models of very complex dynamic objects. Therefore, this method is used to describe electrical power systems.
2. The developed mathematical model of the ultrahigh voltage switch taking into account the virtual simplified kinematic scheme of replacement of the mechanism of movement of contacts, allows to reproduce with a sufficient level of adequacy transient electromagnetic and mechanical processes in the switch taking into account physical principles of switching. In this case, this also applies to the rupture of the current function not only during its transition through zero, but also in a fairly wide time range around zero.
3. The results of the computer simulation presented in this paper fully confirm the theories of transient processes in gas switches, which are complicated high voltage power systems.
REFERENCES
[1] A. Ahmethodžić, M. Kapetanović, and Z. Gajić, «Computer Simulation of High-voltage SF6 Circuit Breakers: Approach to Modeling and Application Results,» IEEE Transactions on Dielectrics and Electrical Insulation, 2011. 18, (4), р. 1314 – 1322.
[2] A. Chaban, A. Szafraniec, and V. Levoniuk, «Mathematical modelling of transient processes in power systems considering effect of high-voltage circuit breakers,» Przeglad elektrotechniczny, 2019. 1, р. 49 – 52.
[3] A. Chaban, «Zasada Hamiltona-Ostrogradskiego w układach elektromechanicznych,» Publisher T. Soroki, Lviv, 2015. (Ukr).
[4] P. Stakhiv, «Discrete mathematical macromodel of electric transmission,» Przegląd Elektrotechniczny, 2013. 4, p. 272-274.
[5] I. Naumkin, M. Balabin, N. Lavrushenko, and R. Naumkin, «Simulation of the 500 kV SF6 circuit breaker cutoff process during the unsuccessful three-phase autoreclosing,» Proceedings of International Conference on power systems Transients, Kyoto, Japan, June 14-17, 2011. р. 5 – 11.
[6] V. Kuchanskyi, «Controlled switching SF6 breakers in the main power electrical grids,» Proceedings of the IED NASU, 2017. 48, р. 38 – 42.
[7] P. Dehghanian, and M. Kezunovic, «Probabilistic impact of transmission line switching on power system operating states,» Proceedings of International Conference on Transmission and Distribution and Exposition (T&D), 2016.
[8] D. Lin, H. Wang, and S. Shen, «An adaptive reclosure scheme for parallel transmission lines with shunt reactors,» Proceedings of International Conference on Transmission and Distribution and Exposition (T&D), 2016.
[9] A. Chaban, V. Levoniuk at all, «Mathematical model of electromagnetic processes in Lehera line at open-circuit operation,» Electrical Engineering & Electromechanics, 2016, 3, p. 30 – 35.
[10] K. Pomorski, «Theoretical mechanics,» Publisher Maria CurieSkłodowska University, Lublin, 2000. (Pol).
[11] V. Sidorets, and I. Pentegov, «Deterministic chaos in nonlinear circuits with an electric arc», Publisher Welding, Kiev, 2013. (Rus).
Authors: dr hab. inż. Andriy Czaban, prof. UTH Rad., University of Technology and Humanities in Radom, Faculty of Transport and Electrical Engineering, ul. Malczewskiego 29, 26-600 Radom, E-mail: atchaban@gmail.com; Ph.D. Vitaliy Levoniyk, Lviv National Agrarian University, Department of Electrical Systems, 1, V. Velykogo str., 80381 Dubliany, Lviv region, Ukraine, E-mail: Bacha1991@ukr.net; assoc. prof., Ph.D Radosław Figura, University of Technology and Humanities in Radom, Faculty of Transport and Electrical Engineering, ul. Malczewskiego 29, 26-600 Radom, E-mail: r.figura@uthrad.pl.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 97 NR 7/2021. doi:10.15199/48.2021.07.19