Published by Mariusz DRABECKI, Eugeniusz TOCZYŁOWSKI,
Warsaw University of Technology, Institute of Control and Computation Engineering
Abstract. In this paper we analyse a power dispatch method for obtaining feasible power flows, both active and reactive power, in terms of satisfying the transmission, voltage level and voltage angles’ constraints, under assumption that supply of electric power is directly contracted by the market participants in the deregulated environment, through energy trade. The method is based on solving two optimization problems originated from Optimal Power Flow standard formulations, which can be solved by system’s operator. The approach was tested on 9-bus test system, under three different loading scenarios.
Streszczenie W artykule przedstawiono metodę otrzymywania dyspozycji mocy, dającej dopuszczalny rozpływ mocy, zarówno czynnej jak i biernej, przy założeniu, że dostawa energii jest kontraktowana bezpośrednio pomiędzy uczestnikami zderegulowanego rynku. Metoda bazuje na wykorzystywaniu dwóch zadaniach optymalizacji, wyprowadzonych od standardowego zadania typu Optimal Power Flow. Prezentowane podejście zostało przetestowane symulacyjnie na 9-węzłowym systemie testowym, przy trzech różnych scenariuszach obciążenia (Otrzymywanie dopuszczalności rozpływu mocy).
Keywords: deregulated electricity market, Optimal Power Flow, network feasibility of power flow, power systems.
Słowa kluczowe: zderegulowany rynek energii, Optimal Power Flow, dopuszczalność sieciowa rozpływu mocy, systemy elektroenergetyczne
Introduction
In the last decades, we observe trends of transforming the power systems’ architectures from totally controlled by the system operators towards completely deregulated ones, see [1]. In the traditional, centralized approach, generating units are often dispatched by the systems operators who may also participate in contracting supply of electrical energy from market participants. However, this is not the case in the deregulated systems, where it is up to participants to agree on contracts between consumers and suppliers and therefore to allow suppliers to plan the unit self-commitment and self-dispatch of the generation units.
These agreements are likely to be made without considering feasibility issues of the delivery through power flow analyses. As it was shown in [2], network feasibility of power flow (power flows, nodal voltages and angles being within their technical limits), considering both active and reactive flow, depends highly on grid model used for determining the power dispatch. Thus, when units are dispatched basing only on individual participants’ preferences, as in the deregulated systems, it is possible to obtain dispatch that yields an infeasible flow. So, it is important to find a way of obtaining feasible re-dispatch which would take into account individual agreements between market participants.
According to authors of [1,3,4], the technical feasibility issues might be addressed by installing controllable hardware access terminals at generation/load bus level. These devices will need to have capabilities of limiting possible generation/demand of a given market participant to ensure network feasibility of the dispatch.
We shall consider a typical scenario in which the power system under consideration may be a local grid, or a wider area sub-network, managed by the system operator striving for system self-balancing.
Some research has already been conducted in looking for ways of dispatching generating units in distributed and deregulated environments. However, nowadays it is the system operator who knows best all technical limits of the power system. Thus, it is reasonable to assume that, at least in the period of transition from regulated to deregulated architecture, the system’s operator is a relevant entity to guard security and stability of power supply to its customers.
Authors of [4, 5, 6] approached the self-balancing problem by solving optimization problems, such as the economic dispatch or OPF/DC-OPF ones. However, these research works focused solely on minimizing the social welfare function, neglecting contracts made freely between consumers and suppliers of electric power. What is more, in these works the role of system’s operator remains unclear and possibly suppressed.
In the power system under consideration, the system operator for re-dispatching purposes may procure balancing energy from local energy sources/demands, or from a wider area network system which is connected to, and assures central control of the access terminals at the generation/load bus level. The balancing energy can be provided by suppliers, or by consumer`s loads through various demand-side response programs. For simplicity, we neglect option that the system operator procures other balancing services, such as reserves.
In this paper we analyze the approach for central balancing and control of the proposed access devices. System operator may perform the task with the help of solving some network flow optimization problems, to ensure that the resulting dispatch would yield feasible power flows in terms of all technical constraints. The first attempt is based on adjusting levels of generation only at some nodes, while in the second stage joint adjustments of loads and generation are taken into account at all nodes.
For the adjustment tasks we use the network flow formulations that are based on standard Optimal Power Flow (OPF) problem [7] extended to consider contracts signed directly between the market participants without obtaining prior approval from system’s operator.
Proposed approach
In this section the proposed balancing approach is described in detail. As it was already stated, we want to find a way of obtaining network feasible flows, resulting from dispatch, that specifically addresses contracts made directly between market participants, while by-passing operator’s governance.
We shall consider two network flow optimization subproblems formulated further in this section. The first subproblem controls solely generating units only and the second allows also load reductions at the bus level. Both proposed formulations are the restrictions of the standard OPF problem. Thus, any feasible solution of one of these two sub-problems would yield a network feasible power flow in terms of satisfying technical constraints.
In these formulations, contracts made between market participants provide resulted contract positions of the suppliers and loads, and therefore are included as soft limits within the optimization problems, both on generation and demand side.
As contracts are signed directly between market players, overall generation cost (social welfare function) is unknown and is of little interest to the operator. Thus, the cost function can be only comprised of the cost associated with soft violations of the market positions (by adjustments through selling and buying balancing energy at network nodes).
To assure that the resulted power flow is technically feasible, the operator can follow the following generic steps:
0. Accept contracts between suppliers and consumers that lay within all technical limits of generating units, i.e. which do not exceed its technical maxima/minima. Architectural design of an appropriate IT platform is beyond the scope of this article and will not be elaborated.
1. Check the network feasibility of power flow that results from accepted contracts between generators and consumers. If necessary, in case of infeasibility, re-dispatch by adjusting levels of generation only at some nodes. For this purpose we use Formulation (2) of problem described below.
2. If Step 1 does not provide feasible solutions, the reduction of the demand in some nodes may be necessary to obtain feasibility. This can be done jointly by adjustments of both loads and generation in some nodes. For this task we use Formulation (3) described below.
Optimal Power Flow Problem (OPF)
The OPF problems are well-known and widely used nonlinear and non-convex optimization problems, solved by system operators for determining feasible active and reactive power dispatch.
Usually, OPF is a problem of minimizing the total generation cost, with respect to all system constraints such as technical maxima/minima of generating unit constraints, line flow constraints, voltage levels and angle constraints and power balance constraints. However, different other cost functions can be also used, such as: minimization of transmission losses or redispatch of reactive power for enhancing the level of system’s stability such as was done in [8].
Below, in (1), we cite a simplified formulation of the OPF problem as was given in [7,9], with standard cost function i.e. minimization of the overall generation costs:

where: ݂fP – the total cost of generation and transmission, ܰN – set of all buses in the system, ܰNG – set of all generating units, ܰNf – set of all branches in the system, ܲPiinj/ܳQiinj – active / reactive power injection at bus i calculated using standard power flow equations [7], PiD/ܳQiD– active/reactive power demand at bus i, Pi/ܳDi – active/reactive output of unit i, Qimin/max / Pimin/max– generation limits of unit i, Ui – voltage magnitude at bus i, Uimin/max– limits on voltage magnitude of bus i, Θi – voltage angle at bus i, Θimin/max – limits on voltage angles of bus i, Sl – apparent power flow through line l, Slmax– maximum value of apparent power flow through l.
The above standard OPF problem formulation provides the basis for the proposed optimization sub-problem Formulations (2) and (3) described below.
Formulation (2)
Step 1 of the proposed method redispatches generating units to address technical constraints. It is performed by the Operator by solving the following optimization problem (2) Let x be the state of power system. With this notation, mathematical formulation (2) is presented below:

where: CP/Q,iG+/-– positive cost (price) of violation of upper/lower limits on generation of unit i for active/reactive power, SP/Q,iG+/-– slack variable for making violation of limits possible for active/reactive power, CN,i – set of contracts signed with unit i, Pc,ik/Qc,ik – contracted volume of active/reactive power for unit i with contract k, A – feasible set of the standard OPF problem (1). The feasible set of (2) is a restriction of the original OPF, therefore the network feasibility of any feasible solution of (2) is guaranteed. As it can be seen, problem (2) attempts to generate just as much power (both active and reactive) as it was contracted for each customer. However, dispatch based only on contracts may rarely be feasible in terms of transmission constraints. Therefore (2) gives possibility to re-dispatch by adjusting the contracted amounts of generated power by producers in order to find a feasible network flow solution at a minimum cost. By selecting or adjusting prices CP/Q,iG+/-, it is possible for the operator to have impact on selection of units which are preferred to change their generation. In particular, these prices may result from agreements between operator and power producers (subcontracting the balancing energy).
Formulation (3)
If re-dispatching problem (2) is infeasible, it means that possibly too much load was contracted in some nodes. Thus, to find a network feasible solution, reduction of some loads at certain buses might be also necessary. In Formulation (3) of the re-dispatching problem described below this can be done jointly by allowing adjustments of both loads and generation in some nodes.
To model the option of load reduction in the OPF optimization problem, an artificial generator, that represents the load reduction, may be built in each load bus. Capabilities of each of these generation units must be equal at most to the active and reactive load attached to the bus in which the unit is built. The maximum value can be reduced, if needed, if one does not want to shed the load too much for a given consumer.
Let B denote the feasible set of (2). Under such assumption, Formulation (3) is mathematically stated as:

where: NL– set of load buses in the system to be reduced, CP/Q,iL+– positive cost of reducing of load i for active/reactive power ( CP/Q,iG+/-≪ CP/Q,iL+ ), SP/Q,iL+– slack variable for making reduction possible for active/reactive power, PiL/QiL – amount of active/reactive load shed at bus i, PiD/QiD – maximum amount of load reduction.
As it can be seen, re-dispatching problem (3) is more general than problem (2), as problem (2) may be obtained from (3) by setting sufficiently large prices CP/Q,iG+/-, at load nodes to eliminate load reductions. Again, by selecting or adjusting prices CP/Q,iG+/-, it is possible for the Operator to have impact on selection of units which are preferred to change their generation or load.
Simulation results
The performance of the proposed re-dispatching method was illustrated on 9-bus test system given in [9] and available in MATPOWER [10], Its topology is presented in Fig. 1.

The system`s topology is fixed in terms of locations of generation and loading. However, the loading data was modified and randomly distributed across 9-bus system load buses. To investigate the most difficult cases in terms of network feasibility of flows, it was assumed that the contracted generation was distributed among the minimum number of generators to supply the necessary amount of power to the system. It was also assumed that the amount of power required for transmission losses’ compensation was not contracted by consumers – it had to be imposed by the Operator.
The maximum overall generating capabilities of active power are equal to 820 MW with technical minimum of each unit being equal to 10 MW and technical maxima of unit 1, 2 and 3: 250 MW, 300MW, 270 MW respectively. For the purposes of simulation, three overall active power loading scenarios were considered, with load equal to: 30%, 83% and 128% of the maximum generating capabilities in the system. Load itself was distributed randomly across 3 consumer buses. The reactive power loading was kept as in the original data, equal to 115 MVAr. In our tests, for all generating units, we assumed costs CP/Q,iG+/- equal to 100 and CP/Q,iL+ equal to 1000 for all load buses. The problems were implemented using [10]. Scenario 1 In the first test scenario load was equal to 30% of the overall installed capacity in the grid (for active power), i.e. 242.25 MW. Assumption was made that only Generator 1 was fully contracted to cover the loading. This means that it was supposed to output as much power as possible, given the fact that all other units have their technical minima equal to 10 MW. If contracts are made using dedicated platform described in Step 0 of the method, these limits are immediately addressed and units 2 and 3 are contracted for 10 MW and unit 1 for the resulting volume of 222.25 MW. For any contracted positions, solving Formulation (2) of the re-dispatching problem is sufficient to find a feasible flow. Table 1 shows generation results obtained for Scenario 1.
Table 1. Generation in Scenario 1
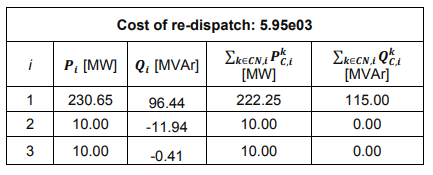
As it can be seen, contracts were correctly taken into consideration by the optimizer. As the contracted flow was technically feasible, only network losses were subject to compensation by Unit 1.
Scenario 2
In this case the loading was set to 83% of system’s installed capacity, i.e. equal to 677.69 MW. This time it was possible to supply necessary amount of power only by contracting all generators installed in the system. By assumption, the first unit to be contracted was unit 1, then unit 2 and as the last one unit 3. Again, the Formulation (2) was sufficient to make the network flow feasible. Obtained generation results are presented in Table 2.
Table 2. Generation in Scenario 2
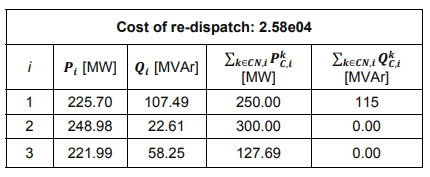
In Scenario 2 more changes in dispatch had to be made to make the network flow feasible. The re-dispatch operation appeared to be about 4 times more costly than in Scenario 1.
Scenario 3
In the third test case loading was set to be 28% higher than the maximum capabilities of installed units and equal to 1051,19 MW. In this case the Formulation (3) had to be solved to find a feasible solution, with all generators contracted. Table 3 shows obtained results for the case when demand in each of the buses was allowed to be reduced by max. 200 MW. Entries with subscript “r” stand for demand reduction in bus i.
Table 3. Generation in Scenario 3
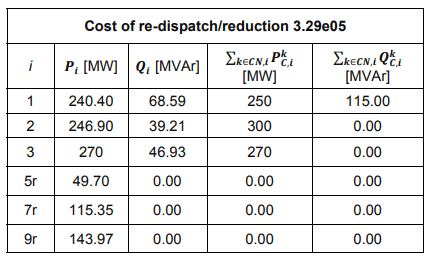
As it can be seen in Table 3, demanded amount of power by consumers has been reduced by the operator by solving re-dispatching problem (3). However, this was accomplished at a rather high, though minimal, cost of redispatch.
Conclusions
In this paper we analyzed an approach to re-direct activity of market players in distributed systems by System Operator, by taking into consideration contracts made between participants and re-dispatching both generation and loads in a manner that yields a feasible power flow in terms of technical limits.
The re-dispatch is obtained at minimum cost by solving one of the two network flow optimization problems in a well-defined order. The problem (2), which controls re-dispatch of supply from the generating units, is supposed to be tried first, and if no feasible solution was found, more general problem (3) is solved, which supports also reducing load demand at bus level. Both formulations are restrictions of the standard Optimal Power Flow problem. Thus, feasibility of their solutions, if such exist, guarantees network feasibility of the corresponding power flows.
The proposed method was illustrated at 9-bus test system, under three different loading scenarios. It was shown that the approach allows System Operator to find network feasible solutions when contracts are made directly between market participants, without deep power flow analyses.
If the re-dispatched solution is different from contracted positions, Operator can either impose necessary changes of dispatch or ask market participants to re-sign their contracts, based on Operator’s directives. Therefore, the output of this paper may be useful either for on-line control of access terminals installed at generator/load bus level or for off-line directing market participants’ activity by giving them feedback information on how to make network feasible contracts.
REFERENCES
[1] Garrity T. F., Innovation and trends for future electric power systems, 2009 Power Systems Conference, Clemson, 2009
[2] Drabecki M., Toczyłowski E., Comparison of three approaches to the security constrained unit commitment problem, Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej, vol. 62, 2019
[3] Popczyk J., Co oznacza inteligentna infrastruktura w cywilizacyjnej transformacji energetyki i gdzie jest jej miejsce?, BPEP Report, Klaster 3×20 Association, Available at: http://klaster3x20.pl/wp-content/uploads/2018/07/2_bpep.pdf, Access: 27/06/2019
[4] Zhang Y., Chow M. Y., Distributed optimal generation dispatch considering transmission losses., 2015 North American Power Symposium (NAPS), Charlotte, 2015,
[5] Kar S., Hug G., Distributed robust economic dispatch: A consensus + innovations approach, 2012 IEEE Power and Energy Society General Meeting, San Diego, 2012
[6] Lin C., Lin S., Distributed optimal power flow with discrete control variables of large distributed power systems, IEEE Transactions on Power Systems, vol. 23, no. 3, 2008
[7] Zhu J, Optimization of Power System Operation, John Wiley & Sons, Hoboken, 2009
[8] Drabecki M., A method for enhancing power system’s steadystate voltage stability level by considering active power optimal dispatch with linear grid models, Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej, vol. 62, 2019
[9] Chow, J. H. (eds.), Time-Scale Modelling of Dynamic Networks with Applications to Power Systems. Lecture Notes in Control and Information Sciences vol. 26, pp. 59 -93, Springer, Berlin, 1982
[10] Zimmerman R. D., Murillo-Sanchez C. E., Thomas R. J., MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education, IEEE Transactions on Power Systems, vol. 26, no. 1, 2011
Authors: Mariusz Drabecki (M.Sc. Eng), E-mail: m.drabecki@onet.eu, Eugeniusz Toczyłowski (Prof. Dr. Sc. Eng), E-mail: e.toczylowski@ia.pw.edu.pl Warsaw University of Technology, Institute of Control and Computation Engineering, Nowowiejska 15/19 st., 00-665 Warszawa, Poland
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 95 NR 10/2019. doi:10.15199/48.2019.10.08