Published by Wojciech BĄCHOREK1, Mariusz BENESZ1, AGH University of Science and Technology (1)
Abstract. This paper presents the influence of distributed generation DG and reclosers placement on the reliability of distribution network. The brute force method and evolutionary algorithm were used to solve the optimization task. The placement of the switches was determined independently using two criteria. The first criterion is the reserve factor, while the second criterion is the SAIDI index. The proposed methods were tested on a real medium voltage distribution system in two variants of operation: with and without DG.
Streszczenie. W artykule przedstawiono wpływ generacji rozproszonej i lokalizacji reklozerów na niezawodność sieci dystrybucyjnej. Zastosowano algorytm przeglądu zupełnego oraz algorytm ewolucyjny. Lokalizację reklozerów ustalono stosując dwa kryteria: współczynnik rezerwowania oraz wskaźnik SAIDI. Obliczenia zrealizowano dla rzeczywistej sieci średniego napięcia. (Wpływ generacji rozproszonej na rozmieszczenie łączników sekcjonujących w sieci średniego napięcia).
Keywords: distribution networks reliability, reclosers, SAIDI, distributed generation.
Słowa kluczowe: niezawodność sieci dystrybucyjnych, łączniki sekcjonujące, SAIDI, generacja rozproszona.
Introduction
One of many important optimization problems solved for distribution networks is the sectionalizing switches placement problem (SPP). This problem is still very important due to the growing popularity of distributed generation sources (DG). Distributed generation improves voltage levels, reduces power losses and improves reliability of the network [1, 2, 3]. Sectionalizing switches, that allow network reconfiguration, should be placed taking into account DG sources. Reconfiguration efficiency is ensured by reclosers [4, 5] and remote-controlled switches [6, 7].
Different methods and objective functions are used to solve the SPP problem. Calculation methods of solving SPP problem may be divided into two groups: based on the classical mathematical methods (for example the mixed integer linear programming [1, 8] or the fuzzy method [9]) and based on the heuristic methods (for example the ant colony optimization algorithm [3, 4, 10], the genetic algorithm [5, 10, 11], the particle swarm optimization method [12, 13] or the taboo search algorithm [14]). Regardless of the calculation method applied, objective functions based on different criteria are assumed. The most applied objective functions are cost criterions and reliability indices. The cost of the switches is taken into account in the articles [3, 4, 12, 14]. The authors of the papers [8, 15] took into account the maintenance costs of switches. In [11], the impact of the cost of DG sources on the placement of sectionalizing switches was considered. SAIDI, SAIFI indices are considered in [4, 9]. The main task of the article is to analyze the placement of sectionalizing switches in the real distribution network with DG. This analysis was carried out independently using two criteria: reserve factor ρ [16, 17] and SAIDI index [4, 9].
The solution sought should correspond to the highest or smallest value of the objective function, respectively for the first and the second criterion. Regardless of the criterion applied, a brute force method and an evolutionary algorithm were used.
First of all, the optimization problem was formulated – the benefits from the installation of sectionalizing switches and the impact of distributed generation on reliability were presented. Next, a description of solution method based on the evolutionary algorithm and a computational example are presented. The calculations were carried out separately for the two selected criteria. In each case, three levels of DG were taken into account.
Problem formulation
A. Idea of sectionalizing switches installation
An example of a simple distribution network is shown in Fig. 1. This is a typical medium voltage power line. Two sectioning switches divide the network into three sections called X, Y and Z. An additional power supply (DG) is connected to the Z section.
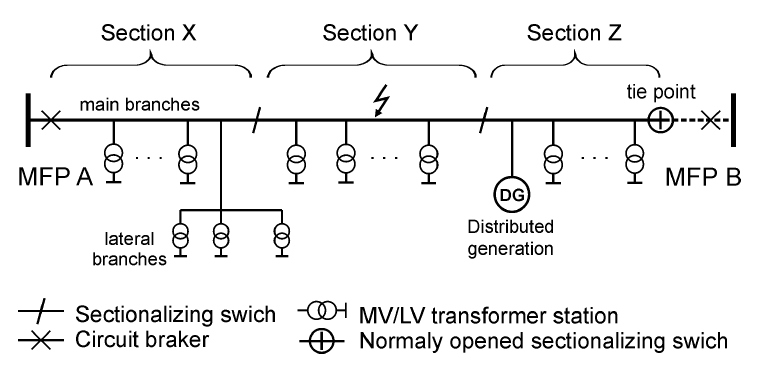
In case of a failure, different scenarios of shutdowns in the network are possible. The first scenario concerns the situation when it is not possible to provide back-up power to the network by closing a switch normally open at the tie point (power supply from MFP B). The second scenario, unlike the first one, assumes the possibility of supplying backup power to the line. In both scenarios, the possibility of a back-up supply using DGs could be considered. This may mean supplying a part of the network only from an additional source (island operation in first scenario) if the load demand of the section to which the DG is connected does not exceed the DG capacity.
In case of a failure of e.g. Y section, the recloser separating X and Y sections is opened and disconnects from the power supply of Y and Z sections. Then, after opening the switch between the Y and Z sections, it is possible to restore power to the Z section. This is possible in the second scenario or in the first scenario with adequate DG capacity.
The proper placement of switches is therefore an important optimisation problem for distribution networks. Sectioning switches ensure reduction of energy not supplied (ENS) [15] to customers and improvement of network reliability indices, which are of interest to Distribution System Operators (DSO).
B. Reserve factor
One of the many criteria for selecting optimal sectionalizing switch placements is the reserve factor ρ (1). This factor was defined and applied in the calculations described e.g. in works [16, 17].
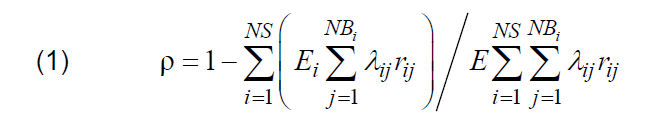
where: E – sum of all customers’ energy in the network, Ei – energy of customers who have been disconnected as a result of a failure in i-th section, NS – number of all sections in the network, NBi – number of branches in the i-th section, λij – average failure rate of j-th branch in i-th section, rij – average outage time of j-th branch in section i.
The minimum value of the reserve factor is 0. The maximum value of the factor is 1. The solutions with the highest reserve factor shall be selected from among all the solutions of the switch placement.
C. SAIDI
The objective function of placement of switches in the distribution network may also be SAIDI index. SAIDI is one of the basic reliability indices used by DSO. This index is calculated and published by DSO on the basis of registered power interruption incidents. SAIDI is an index of an average system duration outages in the supply of electricity expressed in minutes per customer per year. This is a sum of the interruption duration multiplied by number of customers exposed to the effects of the interruption during the year, divided by the number of customers connected to the network (2). Among all the solutions of the switch placement, a solution with the lowest SAIDI value is selected.
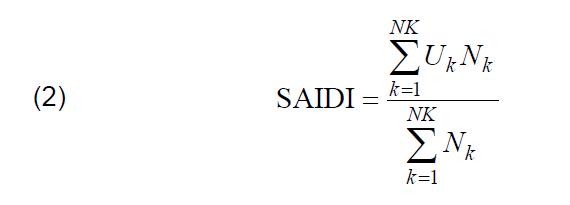
where: NK – number of power delivery points, Nk – number of customers in k-th power delivery point, Uk – annual duration of unscheduled interruptions in k-th point.
The annual duration of unscheduled interruptions Uk is given by (3):

where: NC – total number of possible fault locations, λi – average failure rate of distribution elements grouped together (section), ri – average outage time of distribution elements grouped together.
Index (2) was calculated with a statistical approach based on combinatorial reliability analysis. Dedicated software developed by the authors takes into consideration: the types of sectionalizing switches, their locations and the possibilities of the alternative supply of the line.
Calculation method
In order to determine optimal switch placements, two calculation algorithms were used. If a small number of switches (1 or 2 switches) were assumed, a brute force method (complete overview of the solutions) was carried out. An evolutionary algorithm was used to locate at least 3 sectionalizing switches. This has resulted in a reduction of the calculation time. The solution of a task is written in a form that is “elgible” to the evolutionary algorithm. This is realized with the use of the real coding method.
The solution is expressed in a sequence of numbers called a chromosome (Fig. 2). The number of string elements is equal to the number of placed switches (SN). The location of the switch (SL) in the network is determined at each position of the string in the form of a suitable index.

Their initial population (specified in number) is random. The evolutionary operators are elaborated for creating new solutions. The selection, crossover and mutation operators were used. Stochastic sampling with replacement mechanism was used in the selection procedure. The procedure of a one point crossover of individuals was applied.
The calculations were made using the computer program written in the C ++ programming language.
Case studies
A. The examined MV distribution network
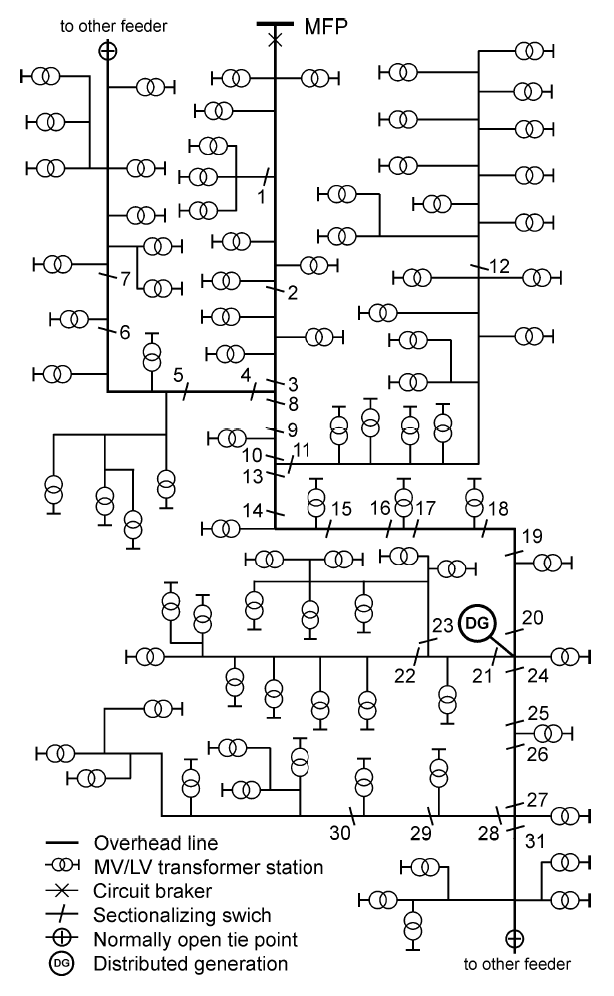
The proposed method is tested on 15 kV modified real-life distribution network located in Poland [17]. The system with 87 MV/LV substations is shown in Fig. 3. This system has 348 possible sectionalizing switches locations. The installation of reclosers is assumed. The total length of the power line is 74.73 km while the lateral branches are 51.98 km. The total peak load 4134 kW. There are 1152 customers connected to the network. The failure rate of MV branches is λ = 0.08 f/yr.km and the mean time to repair is r = 3.83 h/f.
The calculations were carried out in two variants. The first variant assumes that it is not possible to provide backup power to the network by closing the normally open switch. The second one allows such a possibility. Additionally, in a selected point of the network, the connection of a dispersed generation was allowed. The following three power sources were considered: PG1 = 630 kW, PG2 = 1105 kW, PG3 = 2066 kW. These variants of the DG were named respectively G1, G2 and G3. The variant without DG was named as G0.
There are two tie points in the network. They provide the possibility of back-up power supply for the analysed network by closing the normally open switch (tie point). The size of the reserved network depends on the type and place of failure and the number and location of sectionalizing switches. In the power line (Fig. 3) it is not possible to provide backup power to the entire network via a tie points. For more information on backup power limitations, see [17]. In order to solve the task of sectionalizing switches placement, two criteria were applied independently: the maximizing the value of the reserve factor and the minimization of SAIDI. Two scenarios related to the possibility of back-up power supply are being considered:
• scenario I: it is not possible to provide back-up power to the network by closing a switch normally open at the tie point (with and without DG),
• scenario II: backup power supply is possible by closing the switch at the tie point (with and without DG).
The analysed MV power line meets the requirements of the DSO with respect to current load capacity and voltage levels. These requirements are described in the work [17]. The following evolutionary algorithm parameters were chosen: size of population = 24, crossover probability = 0.8, mutation probability = 0.03, number of generations = 3000.
B. Analysis of calculation results
In this chapter, the results of the placement of the reclosers are presented. Calculations were made for two previously described scenarios, in each of them for different number of reclosers. The placement of 1 to 8 switches was assumed. The optimal placement of the switches was determined independently for both criteria ρ (1) and SAIDI (2). The location of the DG source in the medium voltage power line is shown in Fig. 3.
For the analysed network without sectionalizing switches, the reserve factor ρ = 0, SAIDI = 1329.2 min/cus.y. and ENS = 575.5 MWh.
The optimum sectionalizing switch placements according to scenario I for networks without and with DG source have been presented in Table 1. The values of SAIDI have been also shown in Fig. 4.
Table 1. Results of the sectionalizing switch placement (scenario I)
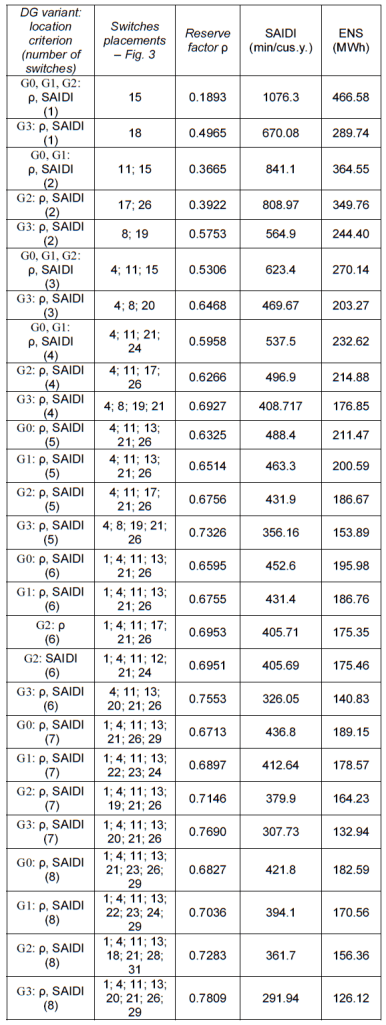
Table 2. Results of the sectionalizing switch placement (scenario II)

The optimum placements of reclosers according to scenario II for networks without and with distributed generation (DG) source have been presented in Table 2. The values of SAIDI have been also shown in Fig. 5.
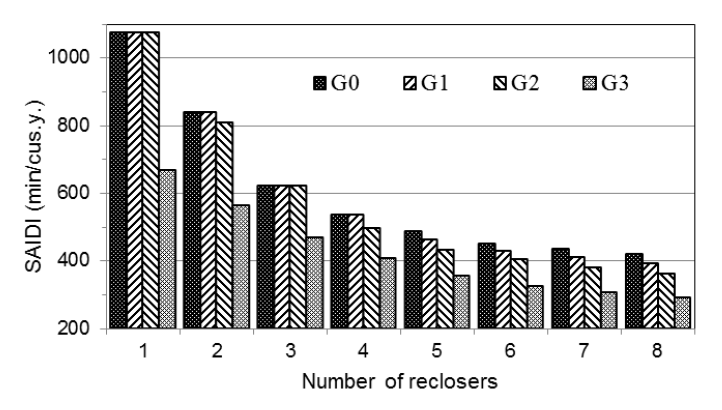
The presented results confirm three directions of improvement of reliability of distribution networks. They rely on: possibility of reconfiguration and back-up supply of the network from other sources than during its normal operation (compare scenario I and scenario II), connection of DG sources to the network (compare variants G0 to G3) and installation of sectioning switches (note the differences in location from 1 to 8 switches) – Fig. 4 and Fig. 5.

In this paper the influence of the number of reclozers and their placements on the value of SAIDI index was analysed. Though reclosers are not always justified economically [17], they significantly reduce the unreliability of the distribution networks. The results obtained for the presented real distribution network confirm the above observations. In this paper, apart from SAIDI results, the results of the reserve factor were presented. For all cases, energy not delivered to consumers was also calculated. The results obtained for both criteria are almost identical in all cases. However, it is not possible to conclude on this basis that both criteria are interchangeable. These indices depend in part on different parameters (see (1) and (2)). This is due to the assumption that there is only one type of customer in the network under analysis, with the same average power demand.
The installation of a DG source improves the reliability indices but the change in the value of the indices depends on the numbers of sections and customers and also the load demand in each section. It can be seen that the calculation algorithm intends to determine the sections in such a way that it would make the best use of the capacity of the source. In other words, in the case of island operation (DG is the only power source), the DG source supplies only those sections whose load demand does not exceed the capacity of the source.
Conclusion
The article solved the problem of the placement of sectionalizing switches (reclosers) in the real medium voltage network. An evolutionary algorithm was used to solve this problem. In addition, the DG source was taken into account. The computational example illustrates tile effectiveness of the proposed method. For the analysed network, almost identical results were obtained by performing independent calculations for two different criteria (reserve factor ρ, SAIDI index). Future research will focus on calculations for many sources of distributed generation in the distribution network.
REFERENCES
[1] Heidari A., Agelidis V.G., Kia M., Considerations of sectionalizing switches in distribution networks with distributed generation, IEEE Trans. Power Del., 30 (2015), no. 3, 1401-1409
[2] Mao Y., Miu K.N., Switch placement to improve system reliability for radial distribution systems with distributed generation, IEEE Trans. Power Syst., 18 (2003), no. 4, 1346-1352
[3] Falaghi H., Haghifam M.R., Singh C., Ant colony optimization-Based method for placement of sectionalizing switches in distribution networks using a fuzzy multiobjective approach, IEEE Trans. Power Del., 24(2009), no. 1, 268-276
[4] Tippachon W, Rerkpreedapong D., Multiobjective optimal placement of switches and protective devices in electric power distribution systems using ant colony optimization, Elect. Power Syst. Res., 79 (2009), 1171-1178
[5] da Silva L.G.W., Pereira R.A.F., Mantovani J.R.S., Optimized allocation of sectionalizing switches and control and protection devices for reliability indices improvement in distribution systems, IEEE/PES Transmission and Distribution Conference and Exposition: Latin America, 2004, 51-56
[6] Xu Y., Liu C.C., Schneider K.P., Ton D.T., Placement of remote-controlled switches to enhance distribution system restoration capability, IEEE Trans. Power Syst., 31 (2016), no.2, 1139-1150
[7] Carvalho P.M.S., Ferreira L.A.F.M., Cerejo da Silva A.J., A decomposition approach to optimal remote controlled switch allocation in distribution systems, IEEE Trans. Power Del., 20 (2005), no.2, 1031-1036
[8] Siirto O.K., Safdarian A., Lehtonen M., Fotuhi-Firuzabad M., Optimal distribution network automation considering earth fault events, IEEE Trans. Smart Grid, 6 (20015), no.2, 1010-1018
[9] Bernardon D.P., Sperandio M., Garcia V.J., Russi J., Canha L.N., Abaide A.R., Daza E.F.B., Methodology for allocation of remotely controlled switches in distribution networks based on a fuzzy multi-criteria decision making algorithm, Elect. Power Syst. Res., 81 (2011), 414-420
[10] Teng J.H., Liu Y.H., A novel ACS-based optimum switch relocation method, IEEE Trans. Power Syst., 18 (2003), no. 1, 113-120
[11]Nematollahi M., Tadayon M., Optimal sectionalizing switches and DG placement considering critical system condition, 21st Iranian Conference on Electrical Engineering (ICEE), 2013, 1-6
[12] Golestani S., Tadayon M., Optimal switch placement in distribution power system using linear fragmented particle swarm optimization algorithm preprocessed by GA, 8th International Conference on the European Energy Market (EEM), Zagreb, Croatia, 25-27 May 2011, pp. 537–542
[13] Bezerra J.R., Barroso G.C., Leão R.P.S., Sampaio R.F., Multiobjective optimization algorithm for switch placement in radial power distribution networks, IEEE Trans. Power Del., 30 (2015), no. 2, 545-552
[14] da Silva L.G.W., R.A. Pereira R.A.F., Rivier Abbad J., Sanches Mantovani J.R., Optimized placement of control and protective devices in electric distribution systems through reactive tabu search algorithm, Elect. Power Syst. Res., 78 (2008), 372-381
[15] Billinton R., Jonnavithula S., Optimal switching device placement in radial distribution system, IEEE Trans. Power Del., 11 (1996), no. 3, 1646-1651
[16] Bąchorek W., Optimal arrangement of sectionalizing switches in medium voltage distribution network, Przegląd Elektrotechniczny, 90 (2014), no. 4, 24-27
[17] Bąchorek W., Benesz M., Influence of Sectionalizing Switches Placement on the Continuity of Customers Power Supply, Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 18-22 June 2018
Authors: dr inż. Wojciech Bąchorek, AGH University of Science and Technology, Faculty of Electrical Engineering, Automatics, Computer Science and Biomedical Engineering, Department of Electrical Engineering and Power Engineering, 30 Mickiewicza Av., 30-059 Krakow, Poland, E-mail: wojbach@agh.edu.pl; dr inż. Mariusz Benesz, AGH University of Science and Technology, Faculty of Electrical Engineering, Automatics, Computer Science and Biomedical Engineering, Department of Electrical Engineering and Power Engineering, 30 Mickiewicza Av., 30-059 Krakow, Poland, E-mail: mariusz.benesz@agh.edu.pl.
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 96 NR 4/2020. doi:10.15199/48.2020.04.24