Published by Salah Belkhir1, Abderrahmane Ziani1, Hakim Azizi2, Hocine Moulai1,
University of Science and Technology Houari Boumediene, Algiers, Algeria (1), University Ziane Achour, Djelfa, Algeria (2) ORCID: 1. 0000-0002-5106-2821
Abstract. The evolvement of the electric and energetic properties of electric arcs at the poles opening of a circuit breaker (CB) is described by nonlinear mathematical models. Most of these models are dimensional types that do not describe the interaction between the arc and the network during the interruption phase. This paper is aimed at the determination of the energy necessary for the arc creation at the opening of a high-voltage circuit breaker with a black box model. The advantage of this model consists of its ability to link the intrinsic characteristics of the arc to the extern blowing (quenching) power. Moreover, it provides fast and stable solving without needing for spatial dimensions of the breaker. The model is applied to a line circuit breaker for which experimental results are available in the literature. Two phases of arc quenching evolvement are evidenced: Constant energy phase followed by a decreasing energy one. The Kema-based model is found to be more accurate for online plasma quenching analysis and the obtained results agree well with experimental ones where the heat energy represents the dominating part.
Streszczenie. Ewolucję właściwości elektrycznych i energetycznych łuków elektrycznych przy otwarciu biegunów wyłącznika opisują nieliniowe modele matematyczne. Większość z tych modeli to modele wymiarowe, które nie opisują interakcji między łukiem a siecią podczas fazy przerwania. Celem artykułu jest określenie energii niezbędnej do wytworzenia łuku przy otwarciu wyłącznika wysokonapięciowego z modelem czarnej skrzynki. Zaletą tego modelu jest możliwość powiązania wewnętrznych charakterystyk łuku z zewnętrzną mocą nadmuchu (gaszenia). Ponadto zapewnia szybkie i stabilne rozwiązywanie bez konieczności wymiarowania przestrzennego wyłącznika. Model stosuje się do wyłącznika liniowego, którego wyniki eksperymentalne są dostępne w literaturze. Wykazano dwie fazy rozwoju gaszenia łuku: faza stałej energii, po której następuje faza malejącej energii. Stwierdzono, że model oparty na Kema jest dokładniejszy do analizy hartowania plazmowego w trybie online, a uzyskane wyniki dobrze zgadzają się z wynikami eksperymentalnymi, w których dominującą część stanowi energia cieplna. (Ocena energii łuku plazmowego w wyłącznikach sieciowych 60 kV)
Keywords: High voltage, circuit breaker, energy, plasma quenching.
Słowa kluczowe: Wysokie napięcie, wyłącznik, energia, hartowanie plazmowe.
Introduction
High voltage circuit breakers (CB) are necessary switchgear for the protection of electrical networks. In both low and high voltage networks, there is a very large number of breaking techniques that use the electric arc as a way to evacuate energy [1-5]. Also, the low cut-off times of less than some milliseconds and the high energy released during the electric arc formation in high voltage circuit breakers make the measurements difficult to achieve and also expensive [6-8]. The development and manufacture of HV circuit breakers require a detailed knowledge of heat transfer mechanisms that evolve at the arc extinction [2, 9, 10]. Although these phenomena are important and of great interest, one notes that only few articles are devoted to.
To extinguish the electric arc appearing at the opening of a high voltage circuit breaker, all the electromagnetic energy stored by the network must be dissipated [1, 11, 12]. Following the high Joule energy released during the CB opening which can reach 30000 J [11, 13, 14], the arc can be cooled through a strong blow of a suitable gas.
In this paper, a power balance has been set up in order to model the energy needed for the creation of the arc during the extinction phase. A precise description of that energy is essential because it determines the dielectric recovery of the arc. The model has been implemented in the Simulink- Matlab environment to determine at first the arc voltage and conductance, and then to calculate the arc creation energies. The model takes into account the ionization time constant of the arc, its voltage, current and even the external blowing power.
Mechanisms of the electric arc formation
Thanks to a mechanical system and as a result of fault current occurrence the high voltage circuit breaker electrodes separate in a quenching chamber. However, after contacts separation, an arc appears and the current continues to flow. In the presence of a gas, this arc is associated to the corresponding plasma.
The filling gas is usually SF6, chosen for its excellent thermal and dielectric properties [11]. The electric arc occurs in the zone of high ionic and electronic density provided from the inter-contacts medium or metal vapors from the circuit breaker poles [2]. The junction zones that bridge the arc column to the contacts are at temperatures close to the melting point of the metal, hence the thermoionic emission is possible [15]. Thus, the electric arc consists of plasma composed of ionized gas and metal vapors.
The arc quenching Models found in the literature [14, 16-20] are always based on Maxwell’s equations, Ohm’s law and the conservation equations of mass and energy. Delalondre et al. [21] developed a two-dimensional code to simulate switching in high voltage circuit breakers. They obtain fields of temperature and potential close to experimental ones. Chevrier et al proposed in [22] a switching arc model in low voltage circuit breakers, while Lindmayer et al [23] have developed a three dimensional model for a low-voltage circuit breaker which predicts the arc movement as a function of temperature and pressure. In addition, Gonzalez [14] adapts a commercial code (Fluent) for thermal plasma behavior in low-voltage circuit breakers. Cassie and Mayr, Lowke et al [24] and Wang et al. [25] have modeled two-dimensional variations of temperature and conductance of quenching arcs in air and SF6. On the other hand, Schavemaker et al [18] and Guardado et al [19] show that a 0D model is sufficient to follow the evolution of arc voltage in high voltage circuit breakers.
Energy balance of the electric arc
The rich bibliography about energy transfer available in [26-33] shows that energy models are based on the conservation equations of mass and energy.
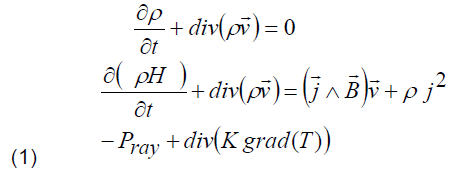
where ρ and H are respectively the density and enthalpy of the plasma, v→ its velocity, j→ the current density, B→ the magnetic field induction, Pray the power lost by radiation and T the thermodynamic temperature.
Experimental measurements have shown that the term (j→ Λ B→) representing the induced current in the arc is often negligible [14], except for vacuum circuit breakers [34]. The appearance of the electric arc of current i(t) at the separation of the contacts creates an arc voltage U(t) that will determine a thermal elementary Joule energy dW during a time dt, thereby producing a very high temperature rise. The expression of this energy is given by:
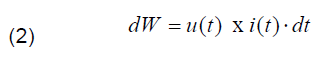
The energy balance per time unit or the power balance reported to the arc in absence of magnetization is expressed by the following relationship:

Where Parc is the total electric power, PJ represents the Joule power provided to the arc which plays a role in the arc temperature rise, P is the cooling capacity due to the blowing of SF6, PC the power lost by thermal conduction and Pray the power dissipated by radiation.
The term PC can be expressed as a function of the arc temperature T and the temperature T0 of the external environment by the following relationship:

where, K is the thermal conductivity of the arc and r its radius.
Even if their dissipation assessment is necessary [35, 36], the terms Pray and PC are usually neglected in black box models calculations [18]. Thus, Pray and PC are estimated to 1% in [21]. Rachard et al [29] reported that the thermal energy dissipated by conduction has moderate influence on the power balance.
New energy model approach
The arc models can be classified into two groups: physical models based on hydrodynamic codes deducted from Navier-Stokes and black box models where the local properties are averaged and their governing equations do not make appear differential terms on the space variables. This is why they are called 0D models. These include the models of Mayr, Cassie and Kema [11, 13].
Also, to follow the energy Q of arc creation in a circuit breaker during its extinction phase, the following assumptions will be adopted. They have been used by several authors [11, 13, 37] in 0D models, namely:
– The arc column is cylindrical in shape.
– The resistivity is constant and its section decreases during extinction.
– The electric field within the arc is constant – The energy of arc creation is proportional to its base surface.
To establish a simple model governing the arc formation, one must assume that the conductance g is only expressed as a function of energy Q used for this arc formation.

Q represents macroscopically the plasma ionization energy [11, 13].
Thanks to a differential equation, we can also write that the difference between the electric power supplied by the network u ⋅ i and the cooling power P injected by blowing is used to create the arc.

where P is the total cooling power provided to the arc, u the arc voltage, i the current through the arc and dt/dQ the power necessary for the arc creation. By expressing the differential of equation (5) as a function of time by multiplying and dividing by the same quantity dQ , we obtain:
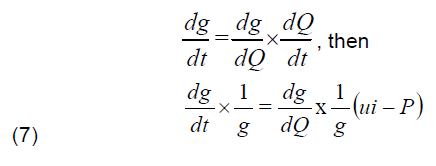
Ohm’s law for a constant electric field E and a current i(t) crossing through an arc of cylindrical geometry and radius R gives for an electric resistivity ρ:

The conductance per unit length of a cylindrical arc can be expressed by:

where S is the surface of arc column. The arc section can be then deduced:
S= g x ρ
The surface of the arc assumed in the Cassie’s assumption [22] has been used to determine the energy Q necessary to create the arc:

One obtains then:

So, we have:

And by substituting the value of Cc by Q/S and the value of g by S/ρ, we obtain:

This equation can be replaced by the logarithmic expressions between Q and g:

Three 0D models (black box) are used to describe the evolution of the term Q through g. By using the Mayr equation, we obtain the following expression:
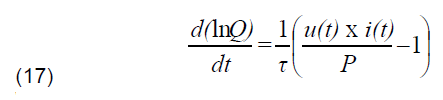
Where, P represents the blowing power in Watts and τ the deionization constant of the blowing gas (SF6).
Similarly, Q can be followed by Cassie equation given by the following expression:

where uc is the Cassie constant voltage. By using the Kema equation, one then obtains:
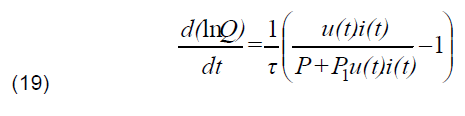
Where P is the external blowing power and P1 a regulation coefficient that is 0.9943. The consecutive arc column surface evolvement is depicted on figure1.
Presentation of the used Electrical network
The HV electrical network used for simulation of breaking arc is shown in Figure 2. Such approach is suitable to take into account external parameters of the CB including the topology of the network and the connected loads [38, 39]. The modelled CB has the same characteristics than that used by Schavemaker et al. [18], namely longitudinal impedance including a resistance and reactance per unit length of the line and two transverse admittances. This network is powered by an electromotive force e = 60 kV. The network characteristics are as follows:
Inductance L=3.5×10-3 H, Resistance R=30 Ω and Capacitance C=2.10-6 F. The frequency is set to 50 Hz. Figure 2 shows the Matlab Simulink synoptic diagram of the studied network. The simulations were performed thanks to the SIMpower SYSTEM tool.
Simulation
In this work, we focused on a typical HV SF6 circuit breaker used in substations and for which experimental results are available in the literature [13, 14, 16-19]. The simulation begins by initializing the arc parameters. The initial conductance g0 of the plasma is first fixed to104 S/m which corresponds to a conducting state. It will allow us to compare our results with those obtained by Schavemaker [18]. The initial energy Q0 is then set to 104 J.


The circuit breaker opening time was set to 0.02 s. The blowing power of SF6 was simulated by the Step block of Simulink with a step equal to the opening time of the circuit breaker. The simulation time was fixed between 0 and 0.03 s to allow comparisons with experimental results available in the literature. Several solvers of differential equations have been tested to obtain the best convergence of the solution to finally choose the ode45/Matlab solver with a variable time step in order to satisfy a relative tolerance of 10-3.
Mayr, Cassie and Kema differential equations solving was made by the use of the Differential Equation Editor (DEE) block. The conductance was replaced by the variable x and the current by the expression u.exp(x). The solutions of the equations are generated in the DEE block as currents that are afterwards injected into the network. The steps followed to solve the Mayr model are presented below. Thus the differential equation was multiplied by the variable u(2) that has been introduced to control the opening time of the circuit breaker by providing a zero signal since the opening time is not reached.

By setting ln(g) = x , we obtain:
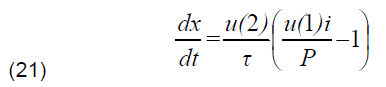
u(2)=0 for a time less than the breaker opening time.
u(2)=1 : For a time greater than or equal to the breaker opening time.
where g is the arc conductance, u(1) the arc voltage and i the arc current.
The output signal is a function of type y= exp(x(1)) x u(1) . To transform it into a usable current, a controlled current source is inserted at the output of the DEE. Figure 3 shows the adopted solving diagram in the Simulink environment.
Results and Interpretations
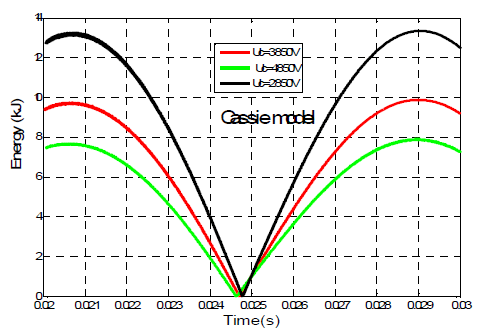
The variations of arc voltage in SF6 through the three models, namely Mayr, Cassie and Kema, for τ = 0.3μs have been plotted on figure 4. The results analysis shows that Mayr model is highly compatible with the Kema model, unlike Cassie model that reproduces constant arc voltages. One observes a voltage peak of about 80 kV which corresponds to the juxtaposition of the transient recovery voltage (TRV) with the numerically calculated voltage presenting good agreement with the experimental values measured by Schavemeker et al. [18] and Guardado et al. [19]. These authors have performed arc voltage measurements at the opening of a high voltage circuit breaker and also observed a sudden voltage increase at the opening of the poles. In Figure 5, the energies of arc creation during the extinction are presented through the model of Mayr. One can note a sudden decrease in energy during the first milliseconds following the arc creation. The shape of the obtained curves depends greatly on the external cooling power P where a fast decrease is observed for P = 30900 W. The numerical solution of Q based on Kema model for three powers is presented on Figure 6. This simulation shows two phases in the evolution of the arc. During the first phase, the creation energy remains constant, while in the second phase, a decrease of this energy is observed. One notes that the energy coupling with the Kema model is better adapted than with Mayr model. In addition, from the results reported in figure 7, i appears that the Cassie model is also not suitable for the simulation of Q. Figure 8 shows the joule heat energy injected during the opening of the circuit breaker poles. There is a rise of the energy necessary to maintain the arc. The injected energy is about 5×105J for Kema and 1.4×105J for Mayr model.



By analysing the obtained results, it appears that the Q energy is about 1% higher than the values of the injected Joule thermal energy. These observations agree well with the results reported by Rachard et al [29] and Van Der Sluis et al. [31]. These authors show that the heat energy of the arc is dominating in high voltage circuit breakers.

Conclusion
A new model of arc creation energy at the opening of high-voltage circuit breakers was developed thanks to acceptable assumptions. Three conductance models were implemented and simulated in Matlab-Simulink environment to retain the best coupling between energy and conductance. The simulations have shown a decrease of the creation energy during the arc extinction phase.
The developed hybrid method has the advantage to no need for spatial dimensions to solve accurately the energy equations. Moreover, the equations are easy to implement and their solving is faster and more stable than the all numerical methods provided by commercial software.
The Kema-based model is found to be more accurate for online plasma quenching analysis where two phases of arc quenching evolvement are evidenced: Constant energy phase followed by a decreasing energy one. The obtained results are found to agree well with experimental ones where the heat energy represents the dominating part.
REFERENCES
[1] T. Chmielewski, P. Oramus, M. Szewczyk, T. Kuczek, W. Piasecki, Circuit breaker models for simulations of short-circuit current breaking and slow-front overvoltages in HV systems, Electric Power Systems Research, 143 (2017) 174-181. DOI: 10.1016/j.epsr.2016.10.046
[2] V. Abbasi, A. Gholami, K. Niayesh, The Effects of SF6-Cu Mixture on the Arc Characteristics in a Medium Voltage Puffer Gas Circuit Breaker due to Variation of Thermodynamic Properties and Transport Coefficients, Plasma Science and Technology, 15 (2013) 586-592. https://doi.org/10.1088/1009-0630/15/6/18
[3] F. Yang, Y. Wu, M.Z. Rong, H. Sun, A.B. Murphy, Z. Ren, C. Niu, Low-voltage circuit breaker arcs—simulation and measurements J. Phys. D: Appl. Phys. 46 (2013) 273001. https://doi.org/10.1088/0022-3727/46/27/273001
[4] M. Mürmann, A. Chusov, R. Fuchs, A. Nefedov, H. Nordborg, Modeling and simulation of the current quenching behavior of a line lightning protection device, J. Phys. D: Appl. Phys. 50 (2017) 105203. doi:10.1088/1361-6463/aa560e
[5] J. Valenta, M. Samohejl, M. Fendrych, P. Kloc, L. Dostál, Diagnostics of Various Phenomena in LV Devices under Real Switching Conditions, Plasma Physics and Technology 4 (2017) 257–260. doi:10.14311/ppt.2017.3.257
[6] T. Cheng, W. Gao, W. Liu and R. Li, Evaluation method of contact erosion for high voltage SF6 circuit breakers using dynamic contact resistance measurement, Electric Power Systems Research, 163 (2017) 725-732. DOI: 10.1016/j.epsr.2017.08.030
[7] D. Dufournet, G.F. Montillet, Transient recovery voltages requirements for system source fault interrupting by small generator circuit breakers, IEEE Trans. Power Delivery, 17 (2002) 474-478. DOI: 10.1109/61.997921
[8] E.A.L. Vianna, A.R. Abaide, L.N. Canha, V. Miranda, Substations SF6 circuit breakers: Reliability evaluation based on equipment condition, Electric Power Systems Research, 142 (2017) 36-46. DOI: 10.1016/j.epsr.2016.08.018
[9] Y. Wu, H. Sun, Y. Tanaka, K. Tomita, M. Rong, F. Yang, Y. Uesugi, T. Ishijima, X. Wang, Y. Feng, Influence of the gas flow rate on the nonchemical equilibrium N2 arc behavior in a model nozzle circuit breaker, J. Phys. D: Appl. Phys., 49 (2016) 425202. https://doi.org/10.1088/0022-3727/49/42/425202
[10] Y. Wu, Y. Cui, J. Duan, H. Sun, C. Wang and C. Niu, Influence of arc current and pressure on non-chemical equilibrium air arc behavior, Plasma Science and Technology, 20 (2017) 014021. https://doi.org/10.1088/2058-6272/aa9325
[11] S. Vacquié, Arc électrique, Techniques de l’Ingénieur, Traité de Génie Electrique D 2870, 1995.
[12] V. Abbasi, A. Gholami, K. Niayesh, Impact of radial external magnetic field on plasma deformation during contact opening in SF6 circuit breakers, Journal of Physics D: Applied Physics, 45 (2012) 415201. https://doi.org/10.1088/0022-3727/45/41/415201
[13] CIGRE Working Group 13-01, Applications of Black Box Modelling to Circuit Breaker, Electra, 149 (1993) 41-71.
[14] J.J. Gonzalez, F. Lago, P. Freton, M. Masquère, X. Franceries, Numerical modelling of an electric arc and its interaction with the anode : Part ii. the three-dimensional model-influence of external forces on the arc column., J. Phys. D : Appl. Phys., 38 (2005) 306–318. https://doi.org/10.1088/0022-3727/38/2/016
[15] X. Liu, S. Wang, Y. Zhou, Z. Wu, K . Xie, N. Wang, Thermal radiation properties of PTFE plasma, Plasma Science and Technology, 19 (2017) 064012. https://doi.org/10.1088/2058-6272/aa65e8
[16] A. Ziani, H. Moulai, Extinction properties of electric arcs in high voltage circuit breakers, Journal of Physics D: Applied Physics, 42 (2009) 105205. https://doi.org/10.1088/0022-3727/42/10/105205
[17] A. Ziani, H. Moulai, 0D Model of thermal exchanges at the opening of an SF6 high voltage circuit breaker, ACTA Press, Proc. of the Int. Conf. on Power and Energy Systems, September 7–9, 2009, Palma de Mallorca, Spain, paper 681-056. http://www.actapress.com/Abstract.aspx?paperId=35434
[18] P.H. Schavemeker, L. Van der Sluis, An improved Mayr type arc model based on current zero measurement, IEEE Trans. Power Delivery, 15 (2000) 580-584. DOI: 10.1109/61.852988
[19] J.L. Guardado, S.G. Maximov, E. Melgoza, J.L. Naredo, P. Moreno, An Improved Arc Model Before Current Zero Based on the Combined Mayr and Cassie Arc Models, IEEE Trans. Power Delivery, 20 (2005) 138-142. DOI: 10.1109/TPWRD.2004.837814
[20] J.B. Belhaouari, Modélisation de l’extinction d’un arc de SF6 hors d’équilibre thermodynamique local, Doctorat thesis, Paul Sabatier university, Toulouse III, France, N°2780, 1997. tel-00003150v2
[21] O. Simonin, C. Delalondre, P.L. Viollet, Modelling in thermal plasma and electric arc column, Pure and Appl. Chem., 64 (1992) 623–628,. DOI: 10.1351/pac199264050623
[22] P. Chévrier, M. Barrault, C. Fiévet, J. Maftoul, J.M. Frémillon, Industrial applications of high-, medium- and low-voltage arc modelling. J. Phys. D: Appl. Phys., 30 (1997) 1346–1355. https://doi.org/10.1088/0022-3727/30/9/010
[23] M. Lindmayer, E. Marzahn, A. Mutzke, M. Springstubbe, Lowvoltage switching arcs – experiments and modeling, 15th Symposium on Physics of Switching Arc, Brno, Czech Republic, 2003.
[24] J.J. Lowke, R.E. Voshall, H.C. Ludwing, Decay of electrical conductance and temperature of arc plasmas, J Appl. Physics, 44 (1973) 3513–3523. DOI: 10.1063/1.1662795
[25] W.Z. Wang, J.D. Yan, M.Z. Rong, A.B. Murphy, J.W. Spencer, Theoretical investigation of the decay of an SF6 gas-blast arc using a two-temperature hydrodynamic model, Journal of Physics D: Applied Physics, 46 (2013) 065203. https://doi.org/10.1088/0022-3727/46/6/065203
[26] M. Razafinimanana, A. Gleizes, F. Mbolidi, S. Vacquié, D. Gravelle, Experimental study of an SF6 arc in extinction, J. Phys. D: Appl. Phys, 23 (1990) 1671. https://doi.org/10.1088/0022-3727/23/12/027
[27] J.C. Lee, Y.J. Kim, SF6 arc plasma modelling for compact and environmental-friendly gas circuit breaker, Surface and Coatings Technology, 201 (2007) 5641-5645. DOI: 10.1016/j.surfcoat.2006.07.110
[28] A. Ziani, H. Moulai, Thermal Transfers of SF6 Electrical Arcs in High Voltage Circuit Breakers, Acta Physica Polonica A, 123 (2012) 241-244. DOI: 10.12693/APhysPolA.123.241
[29] H. Rachard, P. Chévrier, D. Henry, D. Jeandel, Numerical study of coupled electromagnetic and aerothermodynamic phenomena in circuit breaker electric arc, Int. J. Heat and Mass Transfer, 42 (1999) 1723-1734. DOI: 10.1016/S0017-9310(98)00110-0
[30] A. Gleizes, A.M. Rahal, H. DeLacroix, P. Van Doan, Study of a circuit-breaker arc with self-generated flow. I. Energy transfer in the high-current phase, IEEE Transactions on Plasma Science, 16 (1989) 606 – 614. DOI: 10.1109/27.16548
[31] L.Van Der Sluis, W.R. Rutgers, C.G.A. Koreman, A Physical Arc Model for the Simulation of Current Zero Behaviour of High-Voltage Circuit Breakers, IEEE Trans. on Power Delivery, 7 (1992) 1016-1022. DOI: 10.1109/61.127112
[32] N. Osawa, Y. Yoshioka, Analysis of nozzle ablation characteristics of gas circuit breaker, IEEE Trans. Power Del., 25 (2003) 810 – 815. DOI: 10.1109/TDC.2003.1335379
[33] I.M. Dudurych, T. J. Gallagher, E. Rosolowski, Arc effect on single-phase reclosing time of a UHV power transmission line, IEEE Trans. Power Delivery, 19 (2004) 854-860. DOI: 10.1109/TPWRD.2004.824404
[34] Y. Chen, F. Yang, H. Sun, Y. Wu, C. Niu, M. Rong, Influence of the axial magnetic field on sheath development after current zero in a vacuum circuit breaker, Plasma Science and Technology, 19 (2017) 064003. DOI: 10.1088/2058-6272/aa65c8
[35] C. Jan, Y. Cressault, A. Gleizes, K. Bousoltane, Calculation of radiative properties of SF6–C2F4 thermal plasmas—application to radiative transfer in high-voltage circuit breakers modeling, Journal of Physics D: Applied Physics, 47 (2014) 5204. DOI: 10.1088/0022-3727/47/1/015204
[36] S. Tsuda, K. Horinouchi, H. Yugami, Enhancing the radiative heat dissipation from high-temperature SF6 gas plasma by using selective absorbers, Journal of Physics D: Applied Physics, 50 (2017) 365601. DOI: 10.1088/1361-6463/aa7fd5
[37] A. Ziani, H. Moulai, Hybrid model of electric arcs in high voltage circuit breakers, Electric Power Systems Research, 92 (2012) 37-42. DOI: 10.1016/j.epsr.2012.04.021
[38] Joanna Budzisz, The model of a vacuum circuit breaker for switching on capacitor bank, Przegląd Elektrotechniczny, ISSN 0033-2097, R. 95 NR 2/2019, doi:10.15199/48.2019.02.31.
[39] Joanna Budzisz, Zbigniew Wróbleski, The model of a vacuum circuit breaker in MATLAB software for the analysis of overvoltages and overcurrents in capacitive electrical circuits, Przegląd Elektrotechniczny, ISSN 0033-2097, R. 92 NR2/2016, doi:10.15199/48.2016.02.37
Authors: Dr. Salah Belkhir, University of Science and technology Houari Boumediene, Bab Ezzouar, Algiers 16025 Algeria; Email: belkhir.s@hotmail.com; Prof. Abderrahmane Ziani, University of Science and technology Houari Boumediene, Bab Ezzouar, Algiers 16025 Algeria; Email: ziani08@yahoo.fr; Dr. Hakim Azizi, University Ziane Achour, Djelfa, 17000 Algeria; Email: azizihakimbilal@yahoo.fr; Prof. Hocine Moulai, University of Science and technology Houari Boumediene, Bab Ezzouar, Algiers 16025 Algeria; Email: hmoulai@usthb.dz
Source & Publisher Item Identifier: PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 98 NR 10/2022. doi:10.15199/48.2022.10.09